题目内容
【感知】如图①,四边形ABCD、CEFG均为正方形.可知BE=DG.
【拓展】如图②,四边形ABCD、CEFG均为菱形,且∠A=∠F.求证:BE=DG.
【应用】如图③,四边形ABCD、CEFG均为菱形,点E在边AD上,点G在AD延长线上.若AE=2ED,∠A=∠F,△EBC的面积为8,则菱形CEFG的面积为 .

【拓展】如图②,四边形ABCD、CEFG均为菱形,且∠A=∠F.求证:BE=DG.
【应用】如图③,四边形ABCD、CEFG均为菱形,点E在边AD上,点G在AD延长线上.若AE=2ED,∠A=∠F,△EBC的面积为8,则菱形CEFG的面积为

考点:菱形的性质,全等三角形的判定与性质,正方形的性质
专题:
分析:拓展:由四边形ABCD、四边形CEFG均为菱形,利用SAS易证得△BCE≌△DCG,则可得BE=DG;
应用:由AD∥BC,BE=DG,可得S△ABE+S△CDE=S△BEC=S△CDG=8,又由AE=2ED,可求得△CDE的面积,继而求得答案.
应用:由AD∥BC,BE=DG,可得S△ABE+S△CDE=S△BEC=S△CDG=8,又由AE=2ED,可求得△CDE的面积,继而求得答案.
解答:解:拓展:∵四边形ABCD、四边形CEFG均为菱形,
∴BC=CD,CE=CG,∠BCD=∠A,∠ECG=∠F.
∵∠A=∠F,
∴∠BCD=∠ECG.
∴∠BCD-∠ECD=∠ECG-∠ECD,
即∠BCE=∠DCG.
在△BCE和△DCG中,
,
∴△BCE≌△DCG(SAS),
∴BE=DG.(6分)
应用:∵四边形ABCD为菱形,
∴AD∥BC,
∵BE=DG,
∴S△ABE+S△CDE=S△BEC=S△CDG=8,
∵AE=2ED,
∴S△CDE=
×8=
,
∴S△ECG=S△CDE+S△CDG=
,
∴S菱形CEFG=2S△ECG=
.
故答案为:
.(9分)
∴BC=CD,CE=CG,∠BCD=∠A,∠ECG=∠F.
∵∠A=∠F,
∴∠BCD=∠ECG.
∴∠BCD-∠ECD=∠ECG-∠ECD,
即∠BCE=∠DCG.
在△BCE和△DCG中,
|
∴△BCE≌△DCG(SAS),
∴BE=DG.(6分)
应用:∵四边形ABCD为菱形,
∴AD∥BC,
∵BE=DG,
∴S△ABE+S△CDE=S△BEC=S△CDG=8,
∵AE=2ED,
∴S△CDE=
| 1 |
| 3 |
| 8 |
| 3 |
∴S△ECG=S△CDE+S△CDG=
| 32 |
| 3 |
∴S菱形CEFG=2S△ECG=
| 64 |
| 3 |
故答案为:
| 64 |
| 3 |
点评:此题考查了菱形的性质以及全等三角形的判定与性质.此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
计算
-(2014)0+(
)-1的结果为( )
| 9 |
| 1 |
| 2 |
| A、4 | ||
| B、0 | ||
C、
| ||
D、
|
若一个圆锥的侧面展开图是一个半径为10cm,圆心角为252°的扇形,则该圆锥的底面半径为( )
| A、6cm | B、7cm |
| C、8cm | D、10cm |
 如图,已知直线l:y=x,过点A1(1,0)作x轴的垂线交直线l于点B1,以A1 B1为边作正方形A1B1C1A2,过点A2作x轴的垂线交直线l于点B2,以A2 B2为边作正方形A2B2C2A3,…;则点A5的坐标为
如图,已知直线l:y=x,过点A1(1,0)作x轴的垂线交直线l于点B1,以A1 B1为边作正方形A1B1C1A2,过点A2作x轴的垂线交直线l于点B2,以A2 B2为边作正方形A2B2C2A3,…;则点A5的坐标为 ”表示(表示输入、输出操作);“处理框”用“
”表示(表示输入、输出操作);“处理框”用“ ”表示(表示数据处理和运算);“判断框”用“
”表示(表示数据处理和运算);“判断框”用“ ”表示(根据条件决定执行两条路径中的某一条)
”表示(根据条件决定执行两条路径中的某一条)
 如图,在正方形网格中有一等腰△ABC,AB=AC=5,BC=6,请用两种方法画一条直线将△ABC的面积与周长同时平分,要求:
如图,在正方形网格中有一等腰△ABC,AB=AC=5,BC=6,请用两种方法画一条直线将△ABC的面积与周长同时平分,要求: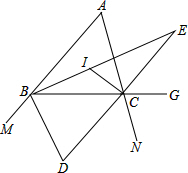 好学的小红在学完三角形的角平分线后,钻研了下列4个问题,请你一起参与,共同进步.
好学的小红在学完三角形的角平分线后,钻研了下列4个问题,请你一起参与,共同进步.