题目内容
如图，EA∥DF，AE=DF，要使△ACE≌△DBF，则只要（ ）| A、AB=CD |
| B、EC=BF |
| C、∠A=∠D |
| D、AB=BC |
考点：全等三角形的判定
专题：
分析：根据AB=CD求出AC=DB，根据平行线的性质得出∠A=∠D，根据SAS推出两三角形全等即可．
解答：解：∵EA∥DF，
∴∠A=∠D，
∵AB=CD，
∴AB+BC=CD+BC，
∴AC=DB，
在△ACE和△DBF中，
，
∴△ACE≌△DBF（SAS），
即只有选项A正确，选项B、C、D都不能推出两三角形全等，
故选：A．
∴∠A=∠D，
∵AB=CD，
∴AB+BC=CD+BC，
∴AC=DB，
在△ACE和△DBF中，
|
∴△ACE≌△DBF（SAS），
即只有选项A正确，选项B、C、D都不能推出两三角形全等，
故选：A．
点评：本题考查了全等三角形的性质和判定的应用，注意：全等三角形的判定定理有SAS，ASA，AAS，SSS，全等三角形的对应边相等，对应角相等．
练习册系列答案
名师金手指领衔课时系列答案
相关题目
如图，Rt△ABC中，∠BAC=90°，AD⊥BC于D，DE⊥AB于E，求证：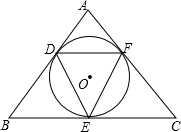
如图，⊙O是△ABC的内切圆，D、E、F是切点，D、E、F分别在AB、BC、CA上．问：△DEF的形状有什么特点？
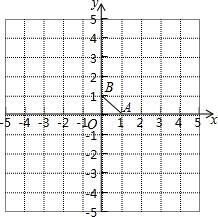如果将点P绕定点M旋转180°后与点Q重合，那么称点P与点Q关于M对称，定点M叫做对称中心．此时，点M是线段PQ的中点．在平面直角坐标系中，△ABO的顶点A，B，O的坐标分别为（1，0）、（0，1）、（0，0）．点列P1、P2、P3、…，中的相邻两点都关于△ABO的一个顶点对称：点P1与点P2关于点A对称，点P2与点P3关于点B对称，点P3与点P4关于点O对称，点P4与点P5关于点A对称，点P5与点P6关于点B对称，点P6与点P7关于点O对称，…，对称中心分别是A，B，O，A，B，O，…，且这些对称中心依次循环．已知点P1的坐标是（1，1），则点P100的坐标为已知抛物线y=ax2+bx+c（a＜0）的对称轴为x=1，交x轴的一个交点为（x1，0），且-1＜x1＜0，有下列5个结论：①abc＞0；②9a-3b+c＜0；③2c＜3b；④（a+c）2＜b2；⑤a+b＞m（am+b）（m≠1的实数）其中正确的结论有（ ）
| A、1个 | B、2个 | C、3个 | D、4个 |
如图所示，已知△ABC中，DE∥BC，AD=2，BD=5，AC=5，求AE的长．下列方程中，属于一元二次方程的是（ ）
| A、ax2+bx+c=0 | ||
B、x2-
| ||
| C、（x+3）2=2（x-3） | ||
| D、（x+4）（x-2）=x2 |