题目内容
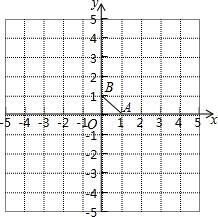 如果将点P绕定点M旋转180°后与点Q重合,那么称点P与点Q关于M对称,定点M叫做对称中心.此时,点M是线段PQ的中点.在平面直角坐标系中,△ABO的顶点A,B,O的坐标分别为(1,0)、(0,1)、(0,0).点列P1、P2、P3、…,中的相邻两点都关于△ABO的一个顶点对称:点P1与点P2关于点A对称,点P2与点P3关于点B对称,点P3与点P4关于点O对称,点P4与点P5关于点A对称,点P5与点P6关于点B对称,点P6与点P7关于点O对称,…,对称中心分别是A,B,O,A,B,O,…,且这些对称中心依次循环.已知点P1的坐标是(1,1),则点P100的坐标为
如果将点P绕定点M旋转180°后与点Q重合,那么称点P与点Q关于M对称,定点M叫做对称中心.此时,点M是线段PQ的中点.在平面直角坐标系中,△ABO的顶点A,B,O的坐标分别为(1,0)、(0,1)、(0,0).点列P1、P2、P3、…,中的相邻两点都关于△ABO的一个顶点对称:点P1与点P2关于点A对称,点P2与点P3关于点B对称,点P3与点P4关于点O对称,点P4与点P5关于点A对称,点P5与点P6关于点B对称,点P6与点P7关于点O对称,…,对称中心分别是A,B,O,A,B,O,…,且这些对称中心依次循环.已知点P1的坐标是(1,1),则点P100的坐标为考点:坐标与图形变化-旋转
专题:规律型
分析:先利用对称中心的定义分别确定P1、P2、P3、P4、P5、P6、P7的坐标,发现点P7的坐标和点P1的坐标相同,即这些点的坐标以6个为一组进行循环,由此可确定点P100的坐标和点P4的坐标相同.
解答:解: ∵点P1的坐标是(1,1),A(1,0),
∵点P1的坐标是(1,1),A(1,0),
而点P1与点P2关于点A对称,
∴点P2的坐标为((1,-1),
同理得到点P3的坐标为((-1,3),
点P4的坐标为(1,-3),
点P5的坐标为((1,3),
点P6的坐标为(-1,-1),
点P7的坐标为(1,1),如图,
∴点P7的坐标和点P1的坐标相同,
∵100=16×6+4,
∴点P100的坐标和点P4的坐标相同,即为(1,-3).
故答案为(1,-3).
 ∵点P1的坐标是(1,1),A(1,0),
∵点P1的坐标是(1,1),A(1,0),而点P1与点P2关于点A对称,
∴点P2的坐标为((1,-1),
同理得到点P3的坐标为((-1,3),
点P4的坐标为(1,-3),
点P5的坐标为((1,3),
点P6的坐标为(-1,-1),
点P7的坐标为(1,1),如图,
∴点P7的坐标和点P1的坐标相同,
∵100=16×6+4,
∴点P100的坐标和点P4的坐标相同,即为(1,-3).
故答案为(1,-3).
点评:本题考查了坐标与图形变化-旋转:图形或点旋转之后要结合旋转的角度和图形的特殊性质来求出旋转后的点的坐标.常见的是旋转特殊角度如:30°,45°,60°,90°,180°.注意从特殊情形中找规律.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,EA∥DF,AE=DF,要使△ACE≌△DBF,则只要( )
如图,EA∥DF,AE=DF,要使△ACE≌△DBF,则只要( )| A、AB=CD |
| B、EC=BF |
| C、∠A=∠D |
| D、AB=BC |
4600000用科学记数法表示,保留三个有效数字,结果是( )
| A、4.60×106 |
| B、4600000 |
| C、4.61×106 |
| D、4.605×106 |
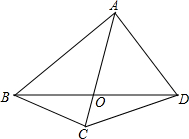 如图,O是四边形ABCD对角线的交点,已知∠BAD+∠BCA=180°,AB=5,AC=4,AD=3,
如图,O是四边形ABCD对角线的交点,已知∠BAD+∠BCA=180°,AB=5,AC=4,AD=3,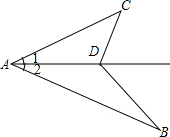 如图,AB>AC,∠1=∠2,求证:AB-AC>BD-CD.
如图,AB>AC,∠1=∠2,求证:AB-AC>BD-CD. 如图,一只蜘蛛沿长方体表面从长方体的一个端点A爬到另一个端点C1,已知长方体的长、宽、高分别是AB=4cm、BC=3cm、CC1=5cm,求蜘蛛爬行的最短距离.
如图,一只蜘蛛沿长方体表面从长方体的一个端点A爬到另一个端点C1,已知长方体的长、宽、高分别是AB=4cm、BC=3cm、CC1=5cm,求蜘蛛爬行的最短距离. 如图所示,DE∥BC,AC=12,AD=
如图所示,DE∥BC,AC=12,AD=