题目内容
11.在等腰Rt△ABC中,AB=AC,∠BAC=90°,点D是斜边BD的中点,点E是线段AB上一动点(点E不与A、B重合),连接DE,作DF⊥DE交AC于点F,连接EF.(1)如图1,如果BC=4,当E是线段AB的中点时,求线段EF的长;
(2)如图2,求证:BC=$\sqrt{2}$(AE+AF);
(3)如图3,点M是线段EF的中点,连接AM,在线段AB上是否存在点E,使得BC=4AM?若存在,求∠EAM的度数;若不存在,请说明理由.
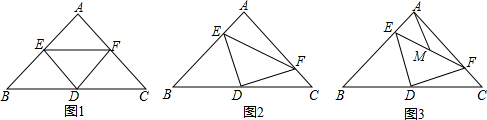
分析 (1)证明点F是AC的中点,可知EF是△AC的中位线即可求出EF的长;
(2)连接AD,证明△ADE≌△CDF,得到AE=CF,根据BC=$\sqrt{2}$AC,等量代换即可得证;
(3)在线段AB存在点E,使得BC=4AM.由BC=4AM,BC=2AD,得到AD=2AM,又在Rt△EAF和Rt△EDF中M是EF的中点,所以AM=DM=$\frac{1}{2}$EF,再由AM+DM≥AD,知2AM≥AD,故只有AM和AD共线时,以上表达式等号才成立,得到∠EAM的度数.
解答 证明:(1)∵点D、E分别是BC、AB的中点,
∴DE∥AC,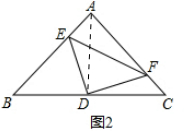
又∵DF⊥DE,∠FDE=90°,
∴∠FDE=∠AED,
∴DF∥AB,
∴点F是AC的中点,
∴EF是△AC的中位线,
∴EF=$\frac{1}{2}$BC=2;
(2)如图2,连接AD,
∵点D是Rt△ABC斜边的中点,
∴AD=$\frac{1}{2}$BC=CD,∠EAD=$\frac{1}{2}$∠BAC=45°,∠ADB=∠ADC=90°,
∵∠C=45°,
∴∠EAD=∠C,
∵∠ADE+∠ADF=90°,∠CDF+∠ADF=90°,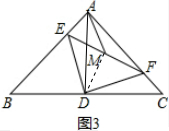
∴∠ADE=∠CDF,
在△ADE和△CDF中
$\left\{\begin{array}{l}{∠EAD=∠C}\\{∠ADE=∠CDF}\\{AD=CD}\end{array}\right.$,
∴△ADE≌△CDF,
∴AE=FC,
∴BC=$\sqrt{2}$AC=$\sqrt{2}$(FC+AF)=$\sqrt{2}$(AE+AF);
(3)在线段AB存在点E,使得BC=4AM.
如图3,连接DM,
∵BC=4AM,BC=2AD,
∴AD=2AM,
∵在Rt△EAF和Rt△EDF中M是EF的中点,
∴AM=DM=$\frac{1}{2}$EF,
∵AM+DM≥AD,
∴2AM≥AD
显然只有AM和AD共线时,以上表达式等号才成立,
此时∠EAM=45°.
点评 本题主要考查了全等三角形的判定与性质、三角形的中位线性质、直角三角形的性质的综合运用,通过辅助线构造全等形和直角三角形斜边中线等于斜边的一半是解决问题的关键.

 如图,在Rt△ABC中,∠BAC=90°,∠ABC的平分线BD交AC于点D,DE是BC的垂直平分线,点E是垂足.已知DC=8,AD=4,则图中长为4$\sqrt{3}$的线段有( )
如图,在Rt△ABC中,∠BAC=90°,∠ABC的平分线BD交AC于点D,DE是BC的垂直平分线,点E是垂足.已知DC=8,AD=4,则图中长为4$\sqrt{3}$的线段有( )
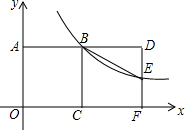 如图,边长为2的正方形ABCO的顶点C、A分别在x轴、y轴上,函数y=$\frac{k}{x}$(x>0)的图象经过点B,把正方形ABCO沿BC翻折得到正方形BCFD,DF交这个函数的图象于点E,连结BE.
如图,边长为2的正方形ABCO的顶点C、A分别在x轴、y轴上,函数y=$\frac{k}{x}$(x>0)的图象经过点B,把正方形ABCO沿BC翻折得到正方形BCFD,DF交这个函数的图象于点E,连结BE. 如图,抛物线y=-x2-2x+3与x轴交于A、B两点,与y轴交于点C,M为抛物线的顶点,点P为x轴负半轴上一点,PC交AM于E,若AE=CE,求点P的坐标.
如图,抛物线y=-x2-2x+3与x轴交于A、B两点,与y轴交于点C,M为抛物线的顶点,点P为x轴负半轴上一点,PC交AM于E,若AE=CE,求点P的坐标.