��Ŀ����
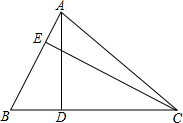
6������ƽ��ֱ������ϵxOy�еĵ�P��ͼ��G���������¶��壺��ͼ��G������������M��N��ʹ��PMNΪ�������Σ����ͼ��GΪ��P�Ħ����ߣ���PΪͼ��G�Ħ��͵㣬��PMNΪͼ��G���ڵ�P�Ħ��������Σ���1����ͼ1����֪��$A��0��-\sqrt{3}��$��B��3��0������ԭ��OΪԲ�ĵġ�O�İ뾶Ϊ1����A��B�����У���O�Ħ��͵��ǵ�A���������ش��O���ڸæ��͵�Ħ��������Σ�������һ�����ɣ�
��2����ͼ2����֪��E��0��2������F��m��0��������m��0�������߶�EFΪԭ��O�Ħ����ߣ����߶�EF����ԭ��O�Ħ��������ε����Ϊ$\frac{{4\sqrt{3}}}{9}$����m��ֵ��
��3����H��0��-2����������y=x2+n�Ħ��͵㣬ֱ��д��n��ȡֵ��Χ��
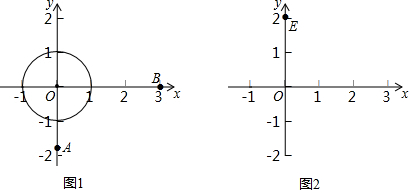
���� ��1�����õȱ������ε��ж����������¶����á�O�Ħ��͵㣻
��2����OL��EF�ڵ�L����ͼ2�������¶��壬���������������ʽ��OL�ij����ɹ��ɶ�����EL�ij�������������Ǻ�����m��
��3����H��0��-2����������y=x2+n�Ħ��͵㣬�ɵá�AHO=30�㣬��OAH=60�㣬�ɱ�ʾ��ͨ��H���ֱ�߽���ʽΪy=$\sqrt{3}$x-2���ɵ�x2+n=$\sqrt{3}$x-2�н�ʱ������H��0��-2����������y=x2+n�Ħ��͵㣬����=3-4��n+2����0���������n��ȡֵ��Χ��
��� �⣺��1����ͼ1��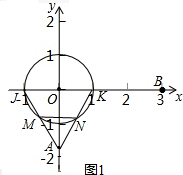
��JK=2��OJ=OK��AO��JK��
��AJ=$\sqrt{A{O}^{2}+J{O}^{2}}$=2��ͬ���ɵã�AK=2��
���AJK��������
ͬ���ɵá�AMNΪ�������Σ�
�ʵ�AΪ��O�Ħ��͵㣬
��ͼ��ͼ1��
��AMN�����AJK��Ϊ��O���ڸæ��͵�Ħ��������Σ�
�ʴ�Ϊ����A��
��2����ͼ2����OL��EF�ڵ�L��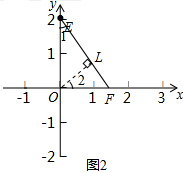
���߶�EFΪ��O�Ħ����ߣ�
��OL��Ϊ�߶�EF���ڵ�O�Ħ��������εĸߣ�
���߶�EF���ڵ�O�Ħ��������ε����Ϊ$\frac{{4\sqrt{3}}}{9}$��
���������εı߳�Ϊ$\frac{4}{3}$��OL=$\frac{2\sqrt{3}}{3}$
��OE=2��OF=m��
��$EL=\sqrt{O{E^2}-O{L^2}}=\sqrt{{2^2}-{{��\frac{{2\sqrt{3}}}{3}��}^2}}=\frac{{2\sqrt{6}}}{3}$��
��$cos��1=\frac{EL}{OE}=\frac{{\sqrt{6}}}{3}$��
��$OF=\frac{OL}{cos��2}=\frac{OL}{cos��1}=\sqrt{2}$��
��$m=\sqrt{2}$��
��3����ͼ3��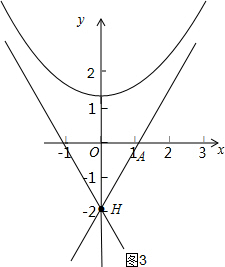
��H��0��-2����������y=x2+n�Ħ��͵㣬
���AHO=30�㣬
���OAH=60�㣬
��ͨ��H���ֱ�߽���ʽΪy=$\sqrt{3}$x-2��
��y=x2+n��
�൱x2+n=$\sqrt{3}$x-2�н�ʱ������H��0��-2����������y=x2+n�Ħ��͵㣬
����=3-4��n+2����0�����n��$-\frac{5}{4}$��
�൱n��$-\frac{5}{4}$ʱ��H��0��-2����������y=x2+n�Ħ��͵㣮
���� ������Ҫ������Բ���ۺ��⣬�漰���ɶ�����һ�κ������������ε����ʣ�����Ĺؼ��Ƕ���ƽ��ֱ������ϵxOy�еĵ�P��ͼ��G�������Ķ��壮

| A�� | m��8 | B�� | m��6 | C�� | 6��m��8 | D�� | 6��m��8 |
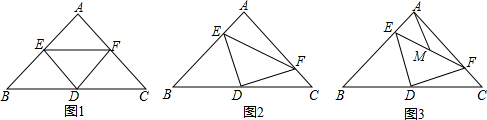
 ��ͼ���ڡ�ABC�У�AB=2��BC=4����ABC�ĸ�AD��CE�ı��Ƕ��٣�����ʾ�����������ε������ʽ��
��ͼ���ڡ�ABC�У�AB=2��BC=4����ABC�ĸ�AD��CE�ı��Ƕ��٣�����ʾ�����������ε������ʽ��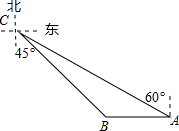 ��ͼ����ͷA����ͷB����������������ͷ֮��ľ���Ϊ32�������һ��������ͷA�������ر�ƫ��60�㷽���е���С��C������ʱ�����ͷB����ƫ��45�㷽������ͷA��С��C�ľ��룮��$\sqrt{3}$��1.732�������ȷ��0.01���
��ͼ����ͷA����ͷB����������������ͷ֮��ľ���Ϊ32�������һ��������ͷA�������ر�ƫ��60�㷽���е���С��C������ʱ�����ͷB����ƫ��45�㷽������ͷA��С��C�ľ��룮��$\sqrt{3}$��1.732�������ȷ��0.01���
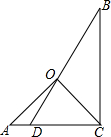 ��ͼ��һ�����ǰ��AOC�͡�BCD��ͼ�ڷţ����AOB=165�㣮
��ͼ��һ�����ǰ��AOC�͡�BCD��ͼ�ڷţ����AOB=165�㣮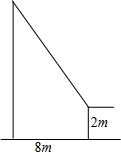 ��ͼ��С�������������������˵ˣ�����ĩ�˸պýӴ������棬Ȼ������ĩ�������������8m�������ִ�ʱ����ĩ�˾������2m������˵ĸ߶�Ϊ17�ף�
��ͼ��С�������������������˵ˣ�����ĩ�˸պýӴ������棬Ȼ������ĩ�������������8m�������ִ�ʱ����ĩ�˾������2m������˵ĸ߶�Ϊ17�ף�