题目内容
3.某商店欲购进A,B两种商品,若购进A种商品5种和B种商品4件需300元,购进A种商品6件和B种商品8件需440元.(1)求A、B两种商品每件的进价分别是多少元?
(2)若该商店每销售1件A种商品可获利8元,每销售1件B种商品可获利6元,该商店准备购进A、B两种商品共50件,且这两种商品全部售出后总获利超过344元,则至少购进多少件A商品?
分析 (1)设A种进价为x元,B种进价为y元.由购进A种商品5件和B种商品4件需300元和购进A种商品6件和B种商品8件需440元建立两个方程,构成方程组求出其解就可以;
(2)设购进A种商品a件,则购进B种商品(50-a)件.根据获得的利润不低于344元,建立不等式求出其解就可以了.
解答 解:(1)设A种进价为x元,B种进价为y元.由题意,得
$\left\{\begin{array}{l}{5x+4y=300}\\{6x+8y=440}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=40}\\{y=25}\end{array}\right.$
答:A种进价为40元,B种进价为25元.
(2)设购进A种商品a件,则购进B种商品(50-a)件.由题意,得
8a+6(50-a)>344,
解得:a>22
∴a的最小整数为23,
答:至少购进A种商品23件.
点评 本题考查了列二元一次方程组解实际问题的运用及二元一次方程组的解法,列一元一次不等式解实际问题的运用及解法,在解答过程中寻找能够反映整个题意的等量关系是解答本题的关键.

练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
8.下列式子正确的是( )
| A. | $\sqrt{16}$=±4 | B. | $\sqrt{(-\frac{1}{3})^{2}}$=$\frac{1}{3}$ | C. | $\sqrt{-1\frac{7}{9}}$=-1$\frac{1}{3}$ | D. | $\root{3}{-9}$=-3 |
15.如果不等式2x-m<0只有三个正整数解,那么m的取值范围是( )
| A. | m<8 | B. | m≥6 | C. | 6<m≤8 | D. | 6≤m<8 |
12.某中学随机抽查了50名学生,了解他们一周的课外阅读时间,结果如表所示:
则这50名学生一周的平均课外阅读时间是5.3小时.
| 时间(小时) | 4 | 5 | 6 | 7 |
| 人数 | 10 | 20 | 15 | 5 |
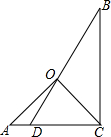 如图,一副三角板△AOC和△BCD如图摆放,则∠AOB=165°.
如图,一副三角板△AOC和△BCD如图摆放,则∠AOB=165°.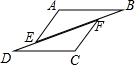 如图,已知B,F,E,D在同一条直线上,AB=CD,AB∥CD,BF=DE,求证:AE=CF.
如图,已知B,F,E,D在同一条直线上,AB=CD,AB∥CD,BF=DE,求证:AE=CF.