题目内容
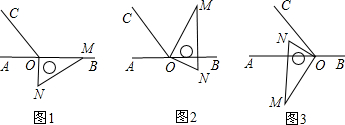
1. 如图,抛物线y=-x2-2x+3与x轴交于A、B两点,与y轴交于点C,M为抛物线的顶点,点P为x轴负半轴上一点,PC交AM于E,若AE=CE,求点P的坐标.
如图,抛物线y=-x2-2x+3与x轴交于A、B两点,与y轴交于点C,M为抛物线的顶点,点P为x轴负半轴上一点,PC交AM于E,若AE=CE,求点P的坐标.
分析 先求出A、C、M的坐标,可知AB=BC,又AE=CE,所以点E在二四象限的角平分线y=-x上,求出直线AM的解析式,再求出y=-x与AM的交点E的坐标,然后求出直线CE的解析式与x轴的交点坐标,即为所求.
解答 解:令y=0,则0=-x2-2x+3,解得:x1=1,x2=-3,
∴A(-3,0),B(1,0),
∵y=-x2-2x+3=-(x+1)2+4,
∴M(-1,4),
∵C(0,3)
∴OA=OC=3,
∵AE=CE,
∴点E在二四象限的角平分线y=-x上,
设直线AM的解析式为y=kx+b,则
$\left\{\begin{array}{l}{-3k+b=0}\\{-k+b=4}\end{array}\right.$
解得:$\left\{\begin{array}{l}{k=2}\\{b=6}\end{array}\right.$,
∴y=2x+6,
由$\left\{\begin{array}{l}{y=-x}\\{y=2x+6}\end{array}\right.$得:$\left\{\begin{array}{l}{x=-2}\\{y=2}\end{array}\right.$,
∴E(-2,2),
设直线CE的解析式为:y=mx+n,则
$\left\{\begin{array}{l}{n=3}\\{-2m+n=2}\end{array}\right.$
解得:$\left\{\begin{array}{l}{m=\frac{1}{2}}\\{n=3}\end{array}\right.$,
∴y=$\frac{1}{2}$x+3,
∵直线CE与x轴交于点P,
∴令y=0,则0=$\frac{1}{2}$x+3,
解得:x=-6,
∴P(-6,0).
点评 本题主要考查了待定系数法求一次函数解析式、数形结合求交点坐标,通过OA=OC,AE=CE发现点E在y=-x上是解决问题的关键.

| 时间(小时) | 4 | 5 | 6 | 7 |
| 人数 | 10 | 20 | 15 | 5 |
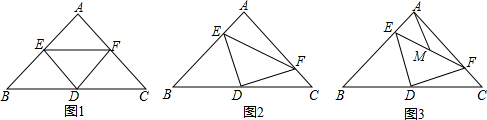
 如图,已知S△ABC=12,AD平分∠BAC,且AD⊥BD于点D,则S△ADC的值是( )
如图,已知S△ABC=12,AD平分∠BAC,且AD⊥BD于点D,则S△ADC的值是( )| A. | 10 | B. | 8 | C. | 6 | D. | 4 |
| A. | 4 | B. | 2$\sqrt{2}$ | C. | $\sqrt{2}$ | D. | 8 |

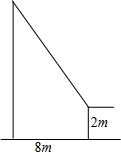 如图,小华将升旗的绳子拉到旗杆底端,绳子末端刚好接触到地面,然后将绳子末端拉到距离旗杆8m处,发现此时绳子末端距离地面2m,则旗杆的高度为17米.
如图,小华将升旗的绳子拉到旗杆底端,绳子末端刚好接触到地面,然后将绳子末端拉到距离旗杆8m处,发现此时绳子末端距离地面2m,则旗杆的高度为17米.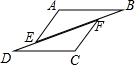 如图,已知B,F,E,D在同一条直线上,AB=CD,AB∥CD,BF=DE,求证:AE=CF.
如图,已知B,F,E,D在同一条直线上,AB=CD,AB∥CD,BF=DE,求证:AE=CF.