题目内容
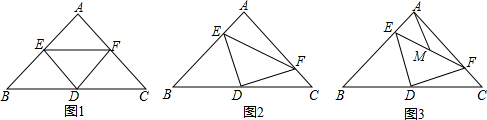
16. 如图,在Rt△ABC中,∠BAC=90°,∠ABC的平分线BD交AC于点D,DE是BC的垂直平分线,点E是垂足.已知DC=8,AD=4,则图中长为4$\sqrt{3}$的线段有( )
如图,在Rt△ABC中,∠BAC=90°,∠ABC的平分线BD交AC于点D,DE是BC的垂直平分线,点E是垂足.已知DC=8,AD=4,则图中长为4$\sqrt{3}$的线段有( )| A. | 4条 | B. | 3条 | C. | 2条 | D. | 1条 |
分析 利用线段垂直平分线的性质得出BE=EC,再利用全等三角形的判定与性质得出AB=BE,进而得出答案.
解答 解:∵∠BAC=90°,∠ABC的平分线BD交AC于点D,DE是BC的垂直平分线,点E是垂足,
∴AD=DE=4,BE=EC,
∵DC=8,AD=4,
∴BE=EC=4$\sqrt{3}$,
在△ABD和△EBD中
$\left\{\begin{array}{l}{∠A=∠BED}\\{∠ABD=∠DBE}\\{BD=DB}\end{array}\right.$,
∴△ABD≌△EBD(AAS),
∴AB=BE=4$\sqrt{3}$,
∴图中长为4$\sqrt{3}$的线段有3条.
故选:B.
点评 此题主要考查了勾股定理以及角平分线的性质以及全等三角形的判定与性质,正确得出BE=AB是解题关键.

练习册系列答案
相关题目
7.已知直线kx+(k+1)y-1=0(k为正整数)与坐标轴所构成的直角三角形的面积为Sk(k=1,2,3,…,2006),则S1+S2+S3+…+S2006=$\frac{1003}{2007}$.
1.若a满足不等式组$\left\{\begin{array}{l}{2a-1≤1}\\{\frac{1-a}{2}>2}\end{array}\right.$,则关于x的方程(a-2)x2-(2a-1)x+a+$\frac{1}{2}$=0的根的情况是( )
| A. | 有两个不相等的实数根 | B. | 有两个相等的实数根 | ||
| C. | 没有实数根 | D. | 以上三种情况都有可能 |
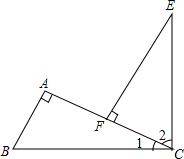 如图,∠A=90°,BC⊥EC,EF⊥AC,BC=CE,你能根据以上的条件,说明△ABC≌△FCE吗?
如图,∠A=90°,BC⊥EC,EF⊥AC,BC=CE,你能根据以上的条件,说明△ABC≌△FCE吗?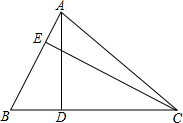 如图,在△ABC中,AB=2,BC=4,△ABC的高AD与CE的比是多少?(提示:利用三角形的面积公式)
如图,在△ABC中,AB=2,BC=4,△ABC的高AD与CE的比是多少?(提示:利用三角形的面积公式)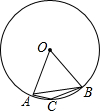 如图,点A,B,C是⊙O上的点,AO=AB,则∠ACB=150度.
如图,点A,B,C是⊙O上的点,AO=AB,则∠ACB=150度.