题目内容
20.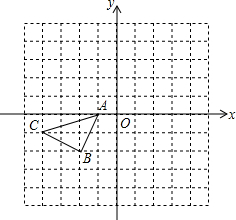 如图所示的正方形网格中,△ABC的顶点均在格点上,请在所给直角坐标系中按要求画图和解答下列问题:
如图所示的正方形网格中,△ABC的顶点均在格点上,请在所给直角坐标系中按要求画图和解答下列问题:(1)将△ABC沿x轴翻折后再沿x轴向右平移1个单位,在图中画出平移后的△A1B1C1.
(2)作△ABC关于坐标原点成中心对称的△A2B2C2.
(3)求B1的坐标(-1,2)C2的坐标(4,1).
分析 (1)根据关于x轴对称的点的坐标特征和点平移后的坐标规律写出点A、B、C的对应点A1、B1、C1的坐标,然后描点得到△A1B1C1;
(2)根据关于原点对称的点的坐标,写出点A、B、C的对应点A2、B2、C2的坐标,然后描点得到△A2B2C2;
(3)由(1)可得B1的坐标,由(2)得C2的坐标.
解答 解:(1)如图,△A1B1C1为所作;
(2)如图,△A2B2C2为所作;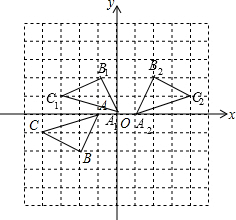
(3)B1(-1,2)C2(4,1).
故答案为(-1,2),(4,1).
点评 本题考查了作图-旋转变换:根据旋转的性质可知,对应角都相等都等于旋转角,对应线段也相等,由此可以通过作相等的角,在角的边上截取相等的线段的方法,找到对应点,顺次连接得出旋转后的图形.也考查了对称性变换.

练习册系列答案
相关题目
10.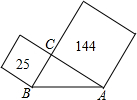 如图,已知在直角三角形ABC中,以直角边BC、AC为边的正方形的面积分别为25、144,则AB的长为( )
如图,已知在直角三角形ABC中,以直角边BC、AC为边的正方形的面积分别为25、144,则AB的长为( )
 如图,已知在直角三角形ABC中,以直角边BC、AC为边的正方形的面积分别为25、144,则AB的长为( )
如图,已知在直角三角形ABC中,以直角边BC、AC为边的正方形的面积分别为25、144,则AB的长为( )| A. | 169 | B. | 119 | C. | 13 | D. | 17 |
 如图,梯子AB靠在墙上,梯子的底端A到墙根O的距离为1m,梯子的顶端B到地面的距离为3m,现将梯子的底端A向外移到A′,使梯子的底端A′到墙根O的距离为2m,同时梯子顶端B下降至B′,那么BB′的长( )
如图,梯子AB靠在墙上,梯子的底端A到墙根O的距离为1m,梯子的顶端B到地面的距离为3m,现将梯子的底端A向外移到A′,使梯子的底端A′到墙根O的距离为2m,同时梯子顶端B下降至B′,那么BB′的长( )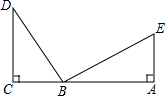 如图,DC⊥CA,EA⊥CA,CD=AB,CB=AE.求证:∠D=∠EBA.
如图,DC⊥CA,EA⊥CA,CD=AB,CB=AE.求证:∠D=∠EBA.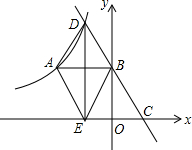 如图所示,在平面直角坐标系中,双曲线y=$\frac{k}{x}$(x<0)上有一点A(-2,2),AB⊥y轴于点B,点C是x轴正半轴上一动点,直线CB交双曲线于点D,DE⊥x轴于点E,连接AE,AD,BE.
如图所示,在平面直角坐标系中,双曲线y=$\frac{k}{x}$(x<0)上有一点A(-2,2),AB⊥y轴于点B,点C是x轴正半轴上一动点,直线CB交双曲线于点D,DE⊥x轴于点E,连接AE,AD,BE.