��Ŀ����
10��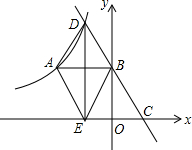 ��ͼ��ʾ����ƽ��ֱ������ϵ�У�˫����y=$\frac{k}{x}$��x��0������һ��A��-2��2����AB��y���ڵ�B����C��x����������һ���㣬ֱ��CB��˫�����ڵ�D��DE��x���ڵ�E������AE��AD��BE��
��ͼ��ʾ����ƽ��ֱ������ϵ�У�˫����y=$\frac{k}{x}$��x��0������һ��A��-2��2����AB��y���ڵ�B����C��x����������һ���㣬ֱ��CB��˫�����ڵ�D��DE��x���ڵ�E������AE��AD��BE����1������C�˶�ʱ���ı���ADBE����״�ܱ������������ܣ������ʱ��C��λ�ã������ܣ�˵�����ɣ�
��2��С������̽�����֣���C�˶���Ӱ���ı���ADBE��״������AD��BE��λ�ù�ϵʼ�ղ��䣬��������������е�ԭ��
���� ��1�����ı���ADBEΪ���Σ���AB��DE���ഹֱƽ�֣���B��D���������ã�Ȼ�����ô���ϵ�������ֱ��BC�Ľ���ʽ���������C�����ꣻ
��2����D�������ǣ�a��-$\frac{4}{a}$�����������ô���ϵ��������������a��ʾ��AD��BE�Ľ���ʽ������ֱ��ƽ�е����������жϣ�
��� �⣺��1�����ı���ADBEΪ���Σ���AB��DE���ഹֱƽ�֣�
������ã�A��-2��2����B��0��2����
���������Ľ���ʽ��y=-$\frac{4}{x}$��E��-1��0��D��-1��4����
��ֱ��BD�Ľ���ʽ��y=kx+b��
��B��0��2����D��-1��4������y=kx+b���ɵã�$\left\{\begin{array}{l}{2=b}\\{4=-k+b}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{k=-2}\\{b=2}\end{array}\right.$��
��ֱ��BD�Ľ���ʽ��y=-2x+2��
����C�������ǣ�1��0����
��2����D�������ǣ�a��-$\frac{4}{a}$����ֱ��AD�Ľ���ʽ��y=kx+b����E��a��0����
��A��-2��2����D��a��-$\frac{4}{a}$������ɵã�$\left\{\begin{array}{l}{-\frac{4}{a}=ka+b}\\{2=-2k+b}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{k=-\frac{2}{a}}\\{b=2-\frac{4}{a}}\end{array}\right.$��
��ֱ��AD�Ľ���ʽ��y=-$\frac{2}{a}$x+��2-$\frac{4}{a}$����
ͬ���ɵ�ֱ��BE�Ľ���ʽ��y=-$\frac{2}{a}$x+2��
��AD��BEʼ��ƽ�У�
���� ���⿼���˴���ϵ������һ�κ�����ֱ�ߵĽ���ʽ����ȷ����a��ʾ��AD��BE�Ľ���ʽ�ǽ������Ĺؼ���

 ����С��ʿ���������ϵ�д�
����С��ʿ���������ϵ�д� ��ͼ��ʾ����һ������Բ���β������������Ʊں���װ�����Ϊ����һ���ݻ���ˮ����ˮƽ���ø�����ʱ��ˮ�����״Ϊ��������
��ͼ��ʾ����һ������Բ���β������������Ʊں���װ�����Ϊ����һ���ݻ���ˮ����ˮƽ���ø�����ʱ��ˮ�����״Ϊ��������| A�� | Բ | B�� | ��Բ | ||
| C�� | һ���ƽ���ı��� | D�� | ���� |
 ��ͼ���뾶Ϊ5�ġ�A�У���BC��ED���Ե�Բ�ĽǷֱ��ǡ�BAC����EAD����֪DE=6����BAC+��EAD=180�㣬����BC�ij����ڣ�������
��ͼ���뾶Ϊ5�ġ�A�У���BC��ED���Ե�Բ�ĽǷֱ��ǡ�BAC����EAD����֪DE=6����BAC+��EAD=180�㣬����BC�ij����ڣ�������| A�� | $\sqrt{41}$ | B�� | $\sqrt{34}$ | C�� | 8 | D�� | 6 |
| A�� | $\root{3}{8}=��2$ | B�� | -$\root{3}{-7}=-\root{3}{7}$ | C�� | $-\sqrt{\frac{16}{9}}=-\frac{4}{3}$ | D�� | $\sqrt{\frac{9}{4}}=��\frac{3}{2}$ |
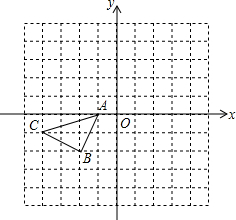 ��ͼ��ʾ�������������У���ABC�Ķ�����ڸ���ϣ���������ֱ������ϵ�а�Ҫ��ͼ�ͽ���������⣺
��ͼ��ʾ�������������У���ABC�Ķ�����ڸ���ϣ���������ֱ������ϵ�а�Ҫ��ͼ�ͽ���������⣺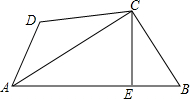 ��ͼ����֪�ı���ABCD�У�ACƽ�֡�BAD��CE��AB�ڵ�E����AE=$\frac{1}{2}$��AB+AD��������D=115�㣬���B=65�㣮
��ͼ����֪�ı���ABCD�У�ACƽ�֡�BAD��CE��AB�ڵ�E����AE=$\frac{1}{2}$��AB+AD��������D=115�㣬���B=65�㣮