题目内容
10．
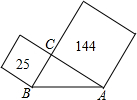如图，已知在直角三角形ABC中，以直角边BC、AC为边的正方形的面积分别为25、144，则AB的长为（ ）| A． | 169 | B． | 119 | C． | 13 | D． | 17 |
分析 由正方形的面积公式可知AC2=144，BC2=25，SM=AB2，在Rt△ABC中，由勾股定理得AC2+BC2=AB2，由此可求SM．即可得出AB的长．
解答 解：∵在Rt△ABC中，由勾股定理得：AC2+BC2=AB2，
又∵AC2=144，BC2=25，SM=AB2，
∴SM=25+144=169，
∴AB=$\sqrt{169}$=13（cm）．
故选C
点评 本题考查了勾股定理及正方形面积公式的运用；解题关键是明确直角三角形的边长的平方即为相应的正方形的面积，难度一般．
练习册系列答案
能力评价系列答案
唐印文化课时测评系列答案
导学与测试系列答案
相关题目
如图，已知矩形ABCD的对角线AC的垂直平分线与边AD、BC分别交于点E、F．若AB=4，BC=8，求四边形AFCE的面积．
18．下列各组3个整数是勾股数的是（ ）
| A． | 4，5，6 | B． | 6，8，9 | C． | 13，14，15 | D． | 8，15，17 |
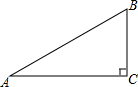已知：如图Rt△ABC中，∠C=90°，AC=$\sqrt{7}$+1，BC=$\sqrt{7}$-1．求：
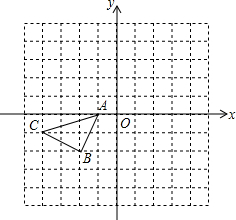如图所示的正方形网格中，△ABC的顶点均在格点上，请在所给直角坐标系中按要求画图和解答下列问题：