题目内容
11. 如图,梯子AB靠在墙上,梯子的底端A到墙根O的距离为1m,梯子的顶端B到地面的距离为3m,现将梯子的底端A向外移到A′,使梯子的底端A′到墙根O的距离为2m,同时梯子顶端B下降至B′,那么BB′的长( )
如图,梯子AB靠在墙上,梯子的底端A到墙根O的距离为1m,梯子的顶端B到地面的距离为3m,现将梯子的底端A向外移到A′,使梯子的底端A′到墙根O的距离为2m,同时梯子顶端B下降至B′,那么BB′的长( )| A. | 小于1m | B. | 等于1m | C. | 大于1m | D. | 以上都不对 |
分析 在Rt△AOB中依据勾股定理可知AB2=10,在Rt△A′OB′中依据勾股定理可求得OB′的长,从而可求得BB′的长.
解答 解:在Rt△AOB中,由勾股定理可知AB2=AO2+OB2=10,
在Rt△A′OB′中由勾股定理可知A′B′2=A′O2+OB′2.
∵AB=A′B′,
∴A′O2+OB′2=10,
∴OB′=$\sqrt{10-4}$=$\sqrt{6}$,
∴BB′=OB-OB′=3-$\sqrt{6}$<1.
故选A.
点评 本题主要考查的是勾股定理的应用,根据梯子的长度不变列出方程是解题的关键.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
3.已知一角形的两边分别为5和9,则此三角形的第三边可能是( )
| A. | 3 | B. | 4 | C. | 9 | D. | 14 |
 如图,已知直线AD,BE相交于点O,∠BOC=90°,OF平分∠AOE,若∠1=35°,求∠2,∠3和∠DOF的度数.
如图,已知直线AD,BE相交于点O,∠BOC=90°,OF平分∠AOE,若∠1=35°,求∠2,∠3和∠DOF的度数.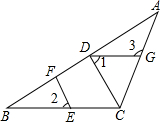 如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F.
如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F. 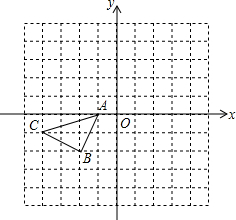 如图所示的正方形网格中,△ABC的顶点均在格点上,请在所给直角坐标系中按要求画图和解答下列问题:
如图所示的正方形网格中,△ABC的顶点均在格点上,请在所给直角坐标系中按要求画图和解答下列问题: