题目内容
12.已知b,c都为1,2,3,…10中的数,若方程x2-bx-c=0至少有一根α也是1,2,3,…10中的数,就称该方程为“漂亮方程”,则“漂亮方程”的个数为( )| A. | 8 | B. | 10 | C. | 12 | D. | 14 |
分析 根据题意,用十字相乘法,先把c分解因数,依据方程根与系数的关系,这两个因数的差就是b,进而可以确定方程,再依次分析c等于1、2、3、…10,分别分析、列举其“漂亮方程”的个数,由加法原理,计算可得答案.
解答 解:用十字相乘法,先把c分解因数,依据方程根与系数的关系,这两个因数的差就是b;
c=1时,有1×(-1)=-1,b=1-1=0不合题意.
c=2 时,有2×(-1)=-2,b=2-1=1,则漂亮方程为x2-x-2=0;
c=3时,有3×(-1)=-3,b=3-1=2,则漂亮方程为x2-2x-3=0;
c=4时,有4×(-1)=-4,b=4-1=3,则漂亮方程为x2-3x-4=0,
c=5时,有5×(-1)=-5,b=5-1=4,则漂亮方程为x2-4x-5=0;
c=6时,有6×(-1)=-6,b=6-1=5,则漂亮方程为x2-5x-6=0,
同时,有2×(-3)=-6,b=3-1=2,则漂亮方程为x2-x-6=0;
c=7时,有7×(-1)=-7,b=7-1=6,则漂亮方程为x2-6x-7=0,
c=8时,有8×(-1)=-8,b=8-1=7,则漂亮方程为x2-7x-8=0,
同时,有(-2)×4=-8,b=4-2=2,则漂亮方程为x2-2x-8=0;
c=9时,有9×(-1)=-9,b=9-1=8,则漂亮方程为x2-8x-9=0;
c=10时,有10×(-1)=-10,b=10-1=9,则漂亮方程为x2-10x-9=0,
同时,有(-2)×5=-10,b=5-2=3,则漂亮方程为x2-3x-10=0;
综合可得,共12个漂亮方程,
故选C.
点评 本题考查一元二次方程根与系数的关系,学会分类计数原理的应用,灵活掌握十字相乘法是解决问题的关键,需要认真审题理解题意,不能漏解.

 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案| A. | 3 | B. | 4 | C. | 9 | D. | 14 |
| A. | -1 | B. | 1 | C. | -1或3 | D. | 1或3 |
 如图,半径为5的⊙A中,弦BC,ED所对的圆心角分别是∠BAC,∠EAD,已知DE=6,∠BAC+∠EAD=180°,则弦BC的长等于( )
如图,半径为5的⊙A中,弦BC,ED所对的圆心角分别是∠BAC,∠EAD,已知DE=6,∠BAC+∠EAD=180°,则弦BC的长等于( )| A. | $\sqrt{41}$ | B. | $\sqrt{34}$ | C. | 8 | D. | 6 |
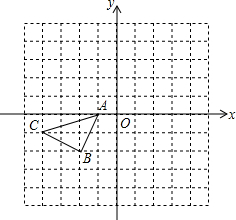 如图所示的正方形网格中,△ABC的顶点均在格点上,请在所给直角坐标系中按要求画图和解答下列问题:
如图所示的正方形网格中,△ABC的顶点均在格点上,请在所给直角坐标系中按要求画图和解答下列问题: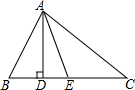 如图,在△ABC中,AD⊥BC,AE平分∠BAC,∠B=80°,∠C=40°;
如图,在△ABC中,AD⊥BC,AE平分∠BAC,∠B=80°,∠C=40°;