题目内容
10.当x≠2时,分式$\frac{2+x}{2-x}$的值存在.分析 根据分式有意义的条件是分母不等于零,求出x的值.
解答 解:根据分式有意义的条件可得2-x≠0,解得x≠2;
当x≠2时,分式有意义;
故答案为2.
点评 本题考查了分式有意义的条件和分式的值.分式有意义的条件是分母不等于零.若分式的值为零,需同时具备两个条件:(1)分子为0;(2)分母不为0.这两个条件缺一不可.

练习册系列答案
相关题目
1.到三角形三边距离相等的点是( )
| A. | 三角形的两条平分线的交点 | |
| B. | 三角形的两条高的交点 | |
| C. | 三角形的三条中线的交点 | |
| D. | 三角形的三条边的垂直平分线的交点 |
2.下列运算正确的是( )
| A. | 2÷$\sqrt{2}$=$\frac{1}{2}$ | B. | $\sqrt{(-2)^{2}}$=-2 | C. | (-$\sqrt{2}$)2=-2 | D. | $\sqrt{2}$×$\sqrt{3}$=$\sqrt{6}$ |
19. 如图是三个反比例函数y=$\frac{{k}_{1}}{x}$,y=$\frac{{k}_{2}}{x}$,y=$\frac{{k}_{3}}{x}$在x轴上方的图象,由此观察得到k1、k2、k3的大小关系为( )
如图是三个反比例函数y=$\frac{{k}_{1}}{x}$,y=$\frac{{k}_{2}}{x}$,y=$\frac{{k}_{3}}{x}$在x轴上方的图象,由此观察得到k1、k2、k3的大小关系为( )
 如图是三个反比例函数y=$\frac{{k}_{1}}{x}$,y=$\frac{{k}_{2}}{x}$,y=$\frac{{k}_{3}}{x}$在x轴上方的图象,由此观察得到k1、k2、k3的大小关系为( )
如图是三个反比例函数y=$\frac{{k}_{1}}{x}$,y=$\frac{{k}_{2}}{x}$,y=$\frac{{k}_{3}}{x}$在x轴上方的图象,由此观察得到k1、k2、k3的大小关系为( )| A. | k1>k2>k3 | B. | k2>k1>k3 | C. | k3>k2>k1 | D. | k3>k1>k2 |
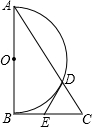 如图,Rt△ABC中,∠ABC=90°,以AB的中点O为圆心、OA长为半径作半圆,交AC于点D,点E为BC的中点,连接DE.
如图,Rt△ABC中,∠ABC=90°,以AB的中点O为圆心、OA长为半径作半圆,交AC于点D,点E为BC的中点,连接DE. 如图,AB为⊙O的切线,切点为B,连接AO,AO与⊙O交于点C,BD为⊙O的直径,连接CD,若∠A=30°,⊙O的半径为2,则图中阴影部分的面积为$\frac{4}{3}$π-$\sqrt{3}$(结果保留π)
如图,AB为⊙O的切线,切点为B,连接AO,AO与⊙O交于点C,BD为⊙O的直径,连接CD,若∠A=30°,⊙O的半径为2,则图中阴影部分的面积为$\frac{4}{3}$π-$\sqrt{3}$(结果保留π)