题目内容
5.等腰三角形中有一边长为5一边长为6,则这个等腰三角形的周长为16或17.分析 由等腰三角形的一边长为6,另一边长为5,可以分别从①若6为底边长,5为腰长,②若5为底边长,6为腰长,去分析,然后根据三角形的三边关系判定是否能组成三角形,继而可求得答案.
解答 解:①若6为底边长,5为腰长,
∵5+5=10>6,
∴5,5,6能组成三角形,
∴它的周长是:5+5+6=16;
②若5为底边长,6为腰长,
∵5+6=15>6,
∴5,6,6能组成三角形,
∴它的周长是:5+6+6=17.
∴它的周长是:16或17.
故答案为:16或17.
点评 此题考查了等腰三角形的性质与三角形的三边关系.此题比较简单,解题的关键是注意分类讨论思想的应用.

练习册系列答案
相关题目
16.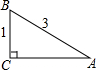 坡比常用来反映斜坡的倾斜程度,如图所示,斜坡AB的坡比为( )
坡比常用来反映斜坡的倾斜程度,如图所示,斜坡AB的坡比为( )
 坡比常用来反映斜坡的倾斜程度,如图所示,斜坡AB的坡比为( )
坡比常用来反映斜坡的倾斜程度,如图所示,斜坡AB的坡比为( )| A. | 1:2$\sqrt{2}$ | B. | 2$\sqrt{2}$:1 | C. | 1:3 | D. | 3:1 |
13.下列叙述正确的是( )
| A. | 画直线AB=10厘米 | |
| B. | 两点之间的线段叫做这两点之间的距离 | |
| C. | 河道改直可以缩短航程,是因为“经过两点有一条直线,并且只有一条直线” | |
| D. | 已知A,B,C三点位于同一条直线上,线段AB=8,BC=5,则AC的长是13或3 |
20.4的平方根是( )
| A. | 2 | B. | 4 | C. | ±2 | D. | ±$\sqrt{2}$ |
17.下列方程中,关于x的一元二次方程是( )
| A. | x2+x+y=0 | B. | $\frac{1}{2}$x2-3x+1=0 | C. | (x+3)2=x3+2x | D. | x2+$\frac{1}{x}$=2 |
15.若△ABC的三边a、b、c满足a2+b2+c2+338=10a+24b+26c,则△ABC的形状为( )
| A. | 锐角三角形 | B. | 直角三角形 | C. | 等腰直角三角形 | D. | 钝角三角形 |
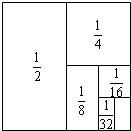 如图,把一个面积为1的正方形等分成两个面积为$\frac{1}{2}$的长方形,接着再把面积为$\frac{1}{2}$的一个长方形分成两个面积为$\frac{1}{4}$的长方形,再把面积为$\frac{1}{4}$的一个长方形分成两个面积为$\frac{1}{8}$的长方形,如此进行下去.
如图,把一个面积为1的正方形等分成两个面积为$\frac{1}{2}$的长方形,接着再把面积为$\frac{1}{2}$的一个长方形分成两个面积为$\frac{1}{4}$的长方形,再把面积为$\frac{1}{4}$的一个长方形分成两个面积为$\frac{1}{8}$的长方形,如此进行下去.