Question

20．如图，AB为⊙O的切线，切点为B，连接AO，AO与⊙O交于点C，BD为⊙O的直径，连接CD，若∠A=30°，⊙O的半径为2，则图中阴影部分的面积为$\frac{4}{3}$π-$\sqrt{3}$（结果保留π）

Answer 1

分析 由条件可求得∠COD的度数，过O作OE⊥CD于点E，则可求得OE的长和CD的长，再利用S_阴影=S_扇形COD-S_△COD可求得答案．

解答 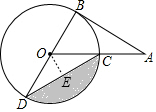解：
如图，过O作OE⊥CD于点E，
∵AB为⊙O的切线，
∴∠DBA=90°，
∵∠A=30°，
∴∠BOC=60°，
∴∠COD=120°，
∵OC=OD=2，
∴∠ODE=30°，
∴OE=1，CD=2DE=2$\sqrt{3}$
∴S_阴影=S_扇形COD-S_△COD=$\frac{120π×{2}^{2}}{360}$-$\frac{1}{2}$×1×2$\sqrt{3}$=$\frac{4}{3}$π-$\sqrt{3}$，
故答案为：$\frac{4}{3}$π-$\sqrt{3}$．

点评 本题主要考查切线的性质和扇形面积的计算，求得扇形COD和△COD的面积是解题的关键．