题目内容
13. 如图,△ABC中,AD是中线,AE是角平分线,CF⊥AE于F,AB=5,AC=2,则$\frac{AF}{EF}$=$\frac{7}{3}$.
如图,△ABC中,AD是中线,AE是角平分线,CF⊥AE于F,AB=5,AC=2,则$\frac{AF}{EF}$=$\frac{7}{3}$.
分析 根据等腰三角形三线合一得到AH=AC、HF=FC,得到DF的△CBH的中位线,求出DF的长,得到$\frac{DF}{AB}$的值,根据平行线分线段成比例定理计算即可.
解答 解: ∵AE是角平分线,CF⊥AE,
∵AE是角平分线,CF⊥AE,
∴AH=AC=2,HF=FC,又BD=DC,
∴DF∥BH,DF=$\frac{1}{2}$BH=$\frac{3}{2}$,
∴$\frac{DF}{AB}$=$\frac{3}{10}$,
∵DF∥BH,
∴$\frac{EF}{EA}$=$\frac{DF}{AB}$=$\frac{3}{10}$,
∴$\frac{AF}{EF}$=$\frac{7}{3}$,
故答案为:$\frac{7}{3}$.
点评 本题考查的是三角形中位线定理和等腰三角形的性质,掌握三角形的中位线平行于第三边且等于第三边的一半是解题的关键.

练习册系列答案
相关题目
5.已知a=b.下列各式中:
①a+5=b+5 ②a-2=b-2
③a+5=b-5 ④2a=b+a
正确的有( )
①a+5=b+5 ②a-2=b-2
③a+5=b-5 ④2a=b+a
正确的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
3.下列各式从左到右的变形属于因式分解的是( )
| A. | ab(a+b-1)=a2b+ab2-ab | B. | a2+1=a(a+$\frac{1}{a}$) | ||
| C. | x2+y2-9=x2+(y+3)(y-3) | D. | -9y2+25x2=(5x+3y)(5x-3y) |
 如图,四边形ABCD中,AB=AD=10,AC平分∠BCD,AE⊥BC于点E,AF⊥CD于CD的延长线上的点F,BC=21,CD=9,求AC的长.
如图,四边形ABCD中,AB=AD=10,AC平分∠BCD,AE⊥BC于点E,AF⊥CD于CD的延长线上的点F,BC=21,CD=9,求AC的长. 如图,菱形ABCD的对角线AC,BD交于点O,以O为圆心,$\frac{1}{2}$AB的长为半径画圆,此圆必过菱形的各边中点,为什么?
如图,菱形ABCD的对角线AC,BD交于点O,以O为圆心,$\frac{1}{2}$AB的长为半径画圆,此圆必过菱形的各边中点,为什么? 如图所示,已知△ABC,过点A作直线l,求作△A′B′C′,使它与△ABC关于l对称,写出作图步骤并作图.
如图所示,已知△ABC,过点A作直线l,求作△A′B′C′,使它与△ABC关于l对称,写出作图步骤并作图.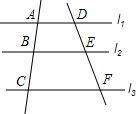 已知,如图,l1∥l2∥l3,下列等式:①$\frac{AB}{AC}$=$\frac{AD}{CF}$;②$\frac{BC}{CA}$=$\frac{EF}{FD}$;③$\frac{AB}{DE}$=$\frac{DF}{AC}$;④$\frac{AB}{DE}$=$\frac{AD}{BE}$;⑤AB:BC:AC=DE:EF:DF,成立的有( )
已知,如图,l1∥l2∥l3,下列等式:①$\frac{AB}{AC}$=$\frac{AD}{CF}$;②$\frac{BC}{CA}$=$\frac{EF}{FD}$;③$\frac{AB}{DE}$=$\frac{DF}{AC}$;④$\frac{AB}{DE}$=$\frac{AD}{BE}$;⑤AB:BC:AC=DE:EF:DF,成立的有( ) 如图所示,在?ABCD中,平行于对角线AC的直线MN分别交DA,DC的延长线于点M,N,交BA,BC于点P,Q.求证:MP=QN.
如图所示,在?ABCD中,平行于对角线AC的直线MN分别交DA,DC的延长线于点M,N,交BA,BC于点P,Q.求证:MP=QN.