题目内容
1. 如图,菱形ABCD的对角线AC,BD交于点O,以O为圆心,$\frac{1}{2}$AB的长为半径画圆,此圆必过菱形的各边中点,为什么?
如图,菱形ABCD的对角线AC,BD交于点O,以O为圆心,$\frac{1}{2}$AB的长为半径画圆,此圆必过菱形的各边中点,为什么?
分析 分别取菱形各边中点E、F、G、H,如图,根据菱形的性质得AC⊥BD,AB=BC=CD=DA,则利用直角三角形斜边上的中线性质得OE=$\frac{1}{2}$AD,OF=$\frac{1}{2}$AB,OG=$\frac{1}{2}$BC,OH=$\frac{1}{2}$CD,所以OE=OF=OG=OH=$\frac{1}{2}$AB,然后根据点与圆的位置关系可判断以O为圆心,$\frac{1}{2}$AB的长为半径画圆,此圆必过菱形的各边中点.
解答 解:分别取菱形各边中点E、F、G、H,如图,
∵四边形ABCD为菱形,
∴AC⊥BD,AB=BC=CD=DA,
∴OE=$\frac{1}{2}$AD,OF=$\frac{1}{2}$AB,OG=$\frac{1}{2}$BC,OH=$\frac{1}{2}$CD,
∴OE=OF=OG=OH=$\frac{1}{2}$AB,
∴以O为圆心,$\frac{1}{2}$AB的长为半径画圆,此圆必过菱形的各边中点
点评 本题考查了菱形的性质:菱形具有平行四边形的一切性质;菱形的四条边都相等;菱形的两条对角线互相垂直,并且每一条对角线平分一组对角.也考查了直角三角形斜边上的中线性质和点与圆的位置关系.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.下列说法中,正确的是( )
| A. | x=5是方程x+5=0的解 | B. | y=5是3y+15=0的解 | ||
| C. | z=-1是-$\frac{z}{4}$=4的解 | D. | x=0.04是方程25x=1的解 |
9.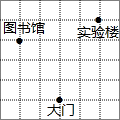 如图所示,每个小方格的边长都为1,在直角坐标系中,如果图书馆的横坐标与实验楼的横坐标互为相反数,大门的纵坐标与实验搂的纵图坐标互为相反数,则图书馆的位置是( )
如图所示,每个小方格的边长都为1,在直角坐标系中,如果图书馆的横坐标与实验楼的横坐标互为相反数,大门的纵坐标与实验搂的纵图坐标互为相反数,则图书馆的位置是( )
 如图所示,每个小方格的边长都为1,在直角坐标系中,如果图书馆的横坐标与实验楼的横坐标互为相反数,大门的纵坐标与实验搂的纵图坐标互为相反数,则图书馆的位置是( )
如图所示,每个小方格的边长都为1,在直角坐标系中,如果图书馆的横坐标与实验楼的横坐标互为相反数,大门的纵坐标与实验搂的纵图坐标互为相反数,则图书馆的位置是( )| A. | (1,5) | B. | (-2,3) | C. | (-2,-1) | D. | (-2,1) |
11.根据下表,回答下列问题.
(1)278.89的平方根是多少?
(2)$\sqrt{259.21}$≈16.1.
(3)$\sqrt{280}$在表中哪两个相邻的数之间?为什么?
| x | 16.0 | 16.1 | 16.2 | 16.3 | 16.4 | 16.5 | 16.6 | 16.7 | 16.8 | 16.9 | 17.0 |
| x2 | 256 | 259.21 | 262.44 | 265.69 | 268.96 | 272.25 | 275.56 | 278.89 | 282.24 | 285.61 | 289 |
(2)$\sqrt{259.21}$≈16.1.
(3)$\sqrt{280}$在表中哪两个相邻的数之间?为什么?
 如图,已知四边形ABCD以及点O.
如图,已知四边形ABCD以及点O. 为扩大绿地面积,要把街心花园的一块长m米,宽a米,向两边分别加宽b米和c米.请你画出草图并用两种方法表示扩大后的绿地面积,思考这两种表示方法有何关系?
为扩大绿地面积,要把街心花园的一块长m米,宽a米,向两边分别加宽b米和c米.请你画出草图并用两种方法表示扩大后的绿地面积,思考这两种表示方法有何关系? 如图所示,已知△ABC中,AD是中线,猜想2AD与AB+AC大小关系,并说明理由.
如图所示,已知△ABC中,AD是中线,猜想2AD与AB+AC大小关系,并说明理由. 如图,△ABC中,AD是中线,AE是角平分线,CF⊥AE于F,AB=5,AC=2,则$\frac{AF}{EF}$=$\frac{7}{3}$.
如图,△ABC中,AD是中线,AE是角平分线,CF⊥AE于F,AB=5,AC=2,则$\frac{AF}{EF}$=$\frac{7}{3}$.