题目内容
4．
如图，四边形ABCD中，AB=AD=10，AC平分∠BCD，AE⊥BC于点E，AF⊥CD于CD的延长线上的点F，BC=21，CD=9，求AC的长．
分析 根据角平分线的性质得到AE=AF，证明Rt△AEB≌Rt△AFD，得到BE=DF，根据CD+DF=BC-BE，求出BE的长，根据勾股定理求出答案．
解答 解：∵AC平分∠BCD，AE⊥BC，AF⊥CD，
∴AE=AF，
在Rt△AEB和Rt△AFD中，
$\left\{\begin{array}{l}{AB=AD}\\{AE=AF}\end{array}\right.$，
∴Rt△AEB≌Rt△AFD（HL），
∴BE=DF，
又∵CE=CF，
∴CD+DF=BC-BE，即9+DF=21-BE，
解得BE=DF=6，则CE=15，
由勾股定理得，AE=$\sqrt{A{B}^{2}-B{E}^{2}}$=8，
∴AC=$\sqrt{A{E}^{2}+E{C}^{2}}$=17．
点评 本题考查的是角平分线的性质、三角形全等的判定和勾股定理，掌握角的平分线上的点到角的两边的距离相等是解题的关键．
练习册系列答案
作业辅导系列答案
相关题目
16．方程$\frac{2x}{x-1}$=1+$\frac{1}{x-1}$的解是（ ）
| A． | x=-1 | B． | x=0 | C． | x=1 | D． | x=2 |
如图，已知四边形ABCD以及点O．
如图，△ABC和△A′B′C′关于点P成中心对称，请确定对称中心点P的位置．
9．
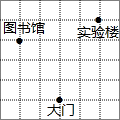如图所示，每个小方格的边长都为1，在直角坐标系中，如果图书馆的横坐标与实验楼的横坐标互为相反数，大门的纵坐标与实验搂的纵图坐标互为相反数，则图书馆的位置是（ ）
如图所示，每个小方格的边长都为1，在直角坐标系中，如果图书馆的横坐标与实验楼的横坐标互为相反数，大门的纵坐标与实验搂的纵图坐标互为相反数，则图书馆的位置是（ ）| A． | （1，5） | B． | （-2，3） | C． | （-2，-1） | D． | （-2，1） |
为扩大绿地面积，要把街心花园的一块长m米，宽a米，向两边分别加宽b米和c米．请你画出草图并用两种方法表示扩大后的绿地面积，思考这两种表示方法有何关系？
如图，△ABC中，AD是中线，AE是角平分线，CF⊥AE于F，AB=5，AC=2，则$\frac{AF}{EF}$=$\frac{7}{3}$．
14．下列变形中正确的是（ ）
| A． | 9-x2+2xy-y2=9-（-x2-2xy+y2） | B． | 9-x2+2xy-y2=9-（x2-2xy-y2） | ||
| C． | 9-x2+2xy-y2=9-（x2-2xy+y2） | D． | 9-x2+2xy-y2=9+（x2-2xy+y2） |