题目内容
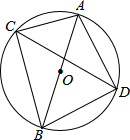 已知:如图所示,AB=10cm,BC=8cm,CD平分∠ACB.
已知:如图所示,AB=10cm,BC=8cm,CD平分∠ACB.(1)求AC和DB的长;
(2)求四边形ACBD的面积.
考点:圆周角定理,勾股定理
专题:
分析:(1)由在⊙O中,直径AB的长为10cm,弦BC=8cm,利用勾股定理,即可求得AC的长,又由CD平分∠ACB交⊙O于点D,可得△ABD是等腰直角三角形,继而求得DB的长;
(2)由S四边形ACBD=S△ABC+S△ABD,即可求得答案.
(2)由S四边形ACBD=S△ABC+S△ABD,即可求得答案.
解答:解:(1)∵AB是⊙O的直径,
∴∠ACB=∠ADB=90°,
∵AB=10cm,BC=8cm,
∴AC=
=6(cm),
∵CD平分∠ACB交⊙O于点D,
∴
=
,
∴AD=BD,
∴∠BAD=∠ABD=45°,
∴DB=
AB=5
cm;
(2)S四边形ACBD=S△ABC+S△ABD=
AC•BC+
AD•BD=24+25=49.
∴∠ACB=∠ADB=90°,
∵AB=10cm,BC=8cm,
∴AC=
| AB2-BC2 |
∵CD平分∠ACB交⊙O于点D,
∴
 |
| AD |
 |
| BD |
∴AD=BD,
∴∠BAD=∠ABD=45°,
∴DB=
| ||
| 2 |
| 2 |
(2)S四边形ACBD=S△ABC+S△ABD=
| 1 |
| 2 |
| 1 |
| 2 |
点评:此题考查了圆周角定理以及勾股定理.此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
在实数
,-
,-3.14,0,π,2.161161116,
中,无理数有( )
| 22 |
| 7 |
| 3 |
| 3 | 64 |
| A、1个 | B、2个 | C、3个 | D、4个 |
 如图,已知AD是△ABC的角平分线,求证:
如图,已知AD是△ABC的角平分线,求证: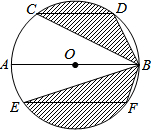 如图,AB是⊙O的直径,CD、EF是⊙O的弦,且AB∥CD∥EF,AB=10,CD=6,EF=8.则图中阴影部分的面积为
如图,AB是⊙O的直径,CD、EF是⊙O的弦,且AB∥CD∥EF,AB=10,CD=6,EF=8.则图中阴影部分的面积为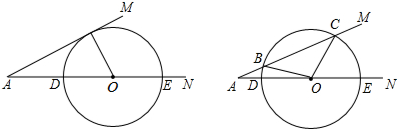
 如图,P是⊙O的直径AB上的一点,PC⊥AB,PC交⊙O于C,∠OCP的平分线交⊙O于D,若点P在半径OA(不包括O点和A点)上移动时,试探究
如图,P是⊙O的直径AB上的一点,PC⊥AB,PC交⊙O于C,∠OCP的平分线交⊙O于D,若点P在半径OA(不包括O点和A点)上移动时,试探究
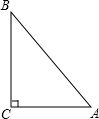 已知:如图,Rt△ABC中,∠C=90°,AC=6,AB=10.
已知:如图,Rt△ABC中,∠C=90°,AC=6,AB=10.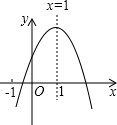 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列4个结论中:①abc>0;②b<a+c;③4a+2b+c>0;④b2-4ac>0;⑤b=2a.正确的是
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列4个结论中:①abc>0;②b<a+c;③4a+2b+c>0;④b2-4ac>0;⑤b=2a.正确的是