题目内容
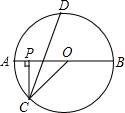 如图,P是⊙O的直径AB上的一点,PC⊥AB,PC交⊙O于C,∠OCP的平分线交⊙O于D,若点P在半径OA(不包括O点和A点)上移动时,试探究
如图,P是⊙O的直径AB上的一点,PC⊥AB,PC交⊙O于C,∠OCP的平分线交⊙O于D,若点P在半径OA(不包括O点和A点)上移动时,试探究 |
| AD |
 |
| BD |
考点:圆心角、弧、弦的关系,平行线的判定与性质
专题:
分析:连OD,由CD平分∠OCP,得到∠1=∠2,而∠1=∠3,所以有OD∥CP,则OD⊥AB,即可得到
=
.
 |
| AD |
 |
| BD |
解答: 解:
解:
=
.理由如下:
连OD,如图,
∵CD平分∠OCP,
∴∠1=∠2,
而OC=OD,有∠1=∠3,
∴∠2=∠3,
∴OD∥CP,
又∵PC⊥AB,
∴OD⊥AB,
∴
=
.
 解:
解: |
| AD |
 |
| BD |
连OD,如图,
∵CD平分∠OCP,
∴∠1=∠2,
而OC=OD,有∠1=∠3,
∴∠2=∠3,
∴OD∥CP,
又∵PC⊥AB,
∴OD⊥AB,
∴
 |
| AD |
 |
| BD |
点评:本题考查了圆周角定理.在同圆或等圆中,同弧和等弧所对的圆周角相等,一条弧所对的圆周角是它所对的圆心角的一半.也考查了垂径定理及平行线的判定与性质.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
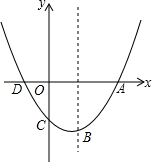 如图,已知抛物线y=
如图,已知抛物线y=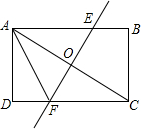 如图所示,将长方形ABCD沿直线EF对折,使顶点A与C重合在一起,折痕EF分别交CD、AB于点F,E交对角线AC相交于点O,已知AB=18cm,BC=12cm.
如图所示,将长方形ABCD沿直线EF对折,使顶点A与C重合在一起,折痕EF分别交CD、AB于点F,E交对角线AC相交于点O,已知AB=18cm,BC=12cm.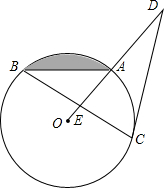 如图,在⊙O中,已知A是劣弧
如图,在⊙O中,已知A是劣弧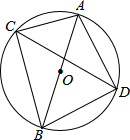 已知:如图所示,AB=10cm,BC=8cm,CD平分∠ACB.
已知:如图所示,AB=10cm,BC=8cm,CD平分∠ACB. 如图所示,在等腰△ABC中,∠C=90°,AC=BC,BE=ED=CF,求∠CEF+∠CAD.
如图所示,在等腰△ABC中,∠C=90°,AC=BC,BE=ED=CF,求∠CEF+∠CAD.