题目内容
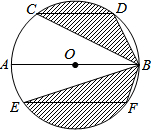 如图,AB是⊙O的直径,CD、EF是⊙O的弦,且AB∥CD∥EF,AB=10,CD=6,EF=8.则图中阴影部分的面积为
如图,AB是⊙O的直径,CD、EF是⊙O的弦,且AB∥CD∥EF,AB=10,CD=6,EF=8.则图中阴影部分的面积为考点:扇形面积的计算
专题:
分析:作直径CG,连接OC、OD、OE、OF、DG、OF,则根据圆周角定理求得DG的长,证明DG=EF,则S扇形ODG=S扇形OEF,然后根据三角形的面积公式证明S△OCD=S△BCD,S△OEF=S△BEF,则S阴影=S扇形OCD+S扇形OEF=S扇形OCD+S扇形ODG=S半圆,即可求解.
解答: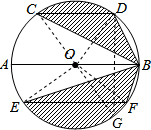 解:作直径CG,连接OC、OD、OE、OF、DG、OF.
解:作直径CG,连接OC、OD、OE、OF、DG、OF.
∵CG是圆的直径,
∴∠CDG=90°,则DG=
=
=8,
又∵EF=8,
∴DG=EF,
∴
=
,
∴S扇形ODG=S扇形OEF,
∵AB∥CD∥EF,
∴S△OCD=S△BCD,S△OEF=S△BEF,
∴S阴影=S扇形OCD+S扇形OEF=S扇形OCD+S扇形ODG=S半圆=
π×52=
π.
故答案是:
π.
 解:作直径CG,连接OC、OD、OE、OF、DG、OF.
解:作直径CG,连接OC、OD、OE、OF、DG、OF.∵CG是圆的直径,
∴∠CDG=90°,则DG=
| CG2-CD2 |
| 102-62 |
又∵EF=8,
∴DG=EF,
∴
 |
| DG |
 |
| EF |
∴S扇形ODG=S扇形OEF,
∵AB∥CD∥EF,
∴S△OCD=S△BCD,S△OEF=S△BEF,
∴S阴影=S扇形OCD+S扇形OEF=S扇形OCD+S扇形ODG=S半圆=
| 1 |
| 2 |
| 25 |
| 2 |
故答案是:
| 25 |
| 2 |
点评:本题考查学生的观察能力及计算能力.本题中找出两个阴影部分面积之间的联系是解题的关键.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
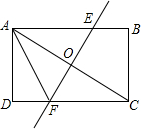 如图所示,将长方形ABCD沿直线EF对折,使顶点A与C重合在一起,折痕EF分别交CD、AB于点F,E交对角线AC相交于点O,已知AB=18cm,BC=12cm.
如图所示,将长方形ABCD沿直线EF对折,使顶点A与C重合在一起,折痕EF分别交CD、AB于点F,E交对角线AC相交于点O,已知AB=18cm,BC=12cm.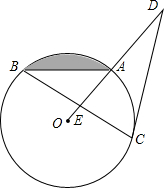 如图,在⊙O中,已知A是劣弧
如图,在⊙O中,已知A是劣弧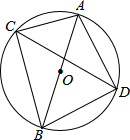 已知:如图所示,AB=10cm,BC=8cm,CD平分∠ACB.
已知:如图所示,AB=10cm,BC=8cm,CD平分∠ACB.