题目内容
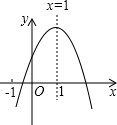 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列4个结论中:①abc>0;②b<a+c;③4a+2b+c>0;④b2-4ac>0;⑤b=2a.正确的是
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列4个结论中:①abc>0;②b<a+c;③4a+2b+c>0;④b2-4ac>0;⑤b=2a.正确的是考点:二次函数图象与系数的关系
专题:
分析:根据开口方向确定a的取值范围,根据对称轴的位置确定b的取值范围,根据抛物线与y轴的交点确定c的取值范围,由乘法法则得到abc的取值范围;根据图象和x=-1及x=2的函数值确定a-b+c及4a+2b+c的取值范围;根据抛物线与x轴交点的个数确定b2-4ac的取值范围;根据对称轴为x=1=-
可以确定b=2a是否成立.
| b |
| 2a |
解答:解:∵抛物线开口向下,
∴a<0,
∵对称轴x=1=-
,
∴b>0,
∵抛物线与y轴的交点在x轴的上方,
∴c>0,
∴abc<0,故①错误;
根据图象知道当x=-1时,y=a-b+c<0,
∴a+c<b,即b>a+c,故②错误;
根据图象知道当x=2时,y=4a+2b+c>0,故③正确;
根据图象知道抛物线与x轴有两个交点,
∴b2-4ac>0,故④正确;
∵对称轴x=1=-
,
∴b=-2a,故⑤错误.
故答案为③④.
∴a<0,
∵对称轴x=1=-
| b |
| 2a |
∴b>0,
∵抛物线与y轴的交点在x轴的上方,
∴c>0,
∴abc<0,故①错误;
根据图象知道当x=-1时,y=a-b+c<0,
∴a+c<b,即b>a+c,故②错误;
根据图象知道当x=2时,y=4a+2b+c>0,故③正确;
根据图象知道抛物线与x轴有两个交点,
∴b2-4ac>0,故④正确;
∵对称轴x=1=-
| b |
| 2a |
∴b=-2a,故⑤错误.
故答案为③④.
点评:此题主要考查了图象与二次函数系数之间的关系,会利用对称轴的范围求2a与b的关系,以及二次函数与方程之间的转换,根的判别式的熟练运用.

练习册系列答案
相关题目
在△ABC中,AB=AC=13,BC=10,则△ABC的面积为( )
| A、30 | B、60 | C、65 | D、120 |
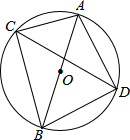 已知:如图所示,AB=10cm,BC=8cm,CD平分∠ACB.
已知:如图所示,AB=10cm,BC=8cm,CD平分∠ACB.
