题目内容
9. 如图,平行四边形ABCD对角线相交于点O,M是AD的中点,连结CM,交BD于点N.则S△AOB:S△CON:S△DMN=3:1:1.
如图,平行四边形ABCD对角线相交于点O,M是AD的中点,连结CM,交BD于点N.则S△AOB:S△CON:S△DMN=3:1:1.
分析 根据平行四边形的性质得到S△AOB=S△COD=$\frac{1}{4}$S平行四边形ABCD,由M是AD的中点,得到S△CDM=$\frac{1}{4}$S平行四边形ABCD,推出S△COD=S△CDM,得到S△CON=S△DMN,根据相似三角形的性质即可得到结论.
解答 解:∵平行四边形ABCD对角线相交于点O,
∴S△AOB=S△COD=$\frac{1}{4}$S平行四边形ABCD,
∵M是AD的中点,
∴S△CDM=$\frac{1}{4}$S平行四边形ABCD,
∴S△COD=S△CDM,
∴S△CON=S△DMN,
∵AD∥BC,
∴△DMN∽△BCN,
∴$\frac{MN}{CN}=\frac{DM}{BC}$=$\frac{1}{2}$,
∴$\frac{{S}_{△DMN}}{{S}_{△CDN}}$=$\frac{1}{2}$,
∴$\frac{{S}_{△DMN}}{{S}_{△CDM}}$=$\frac{1}{3}$,
∴S△DMN=$\frac{1}{12}$S平行四边形ABCD,
∴S△AOB:S△CON:S△DMN=3:1:1.
故答案为:3:1:1.
点评 本题考查了相似三角形的判定和性质,平行四边形的性质,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
相关题目
20. 在平面直角坐标系中,O为原点,点A(-3,0),点B(0,3),点E、点F分别为OA,OB的中点,若正方形OEDF绕点O顺时针旋转,得到正方形OE′D′F′,若直线AE′与直线BF′相交于点P,则点P的纵坐标的最大值是( )
在平面直角坐标系中,O为原点,点A(-3,0),点B(0,3),点E、点F分别为OA,OB的中点,若正方形OEDF绕点O顺时针旋转,得到正方形OE′D′F′,若直线AE′与直线BF′相交于点P,则点P的纵坐标的最大值是( )
 在平面直角坐标系中,O为原点,点A(-3,0),点B(0,3),点E、点F分别为OA,OB的中点,若正方形OEDF绕点O顺时针旋转,得到正方形OE′D′F′,若直线AE′与直线BF′相交于点P,则点P的纵坐标的最大值是( )
在平面直角坐标系中,O为原点,点A(-3,0),点B(0,3),点E、点F分别为OA,OB的中点,若正方形OEDF绕点O顺时针旋转,得到正方形OE′D′F′,若直线AE′与直线BF′相交于点P,则点P的纵坐标的最大值是( )| A. | $\frac{\sqrt{3}+1}{2}$ | B. | $\frac{\sqrt{3}+3}{2}$ | C. | $\frac{\sqrt{3}+3}{4}$ | D. | $\frac{3\sqrt{3}+3}{4}$ |
10.甲乙两家商场平时以同样的价格出售相同的商品.春节期间两家商场都让利酬宾,其中甲商场所有商品按8折出售,乙商场对一次购物中超过200元后的价格部分打7折.
设x(单位:元)表示商品原价,y(单位:元)表示购物金额.
(Ⅰ)根据题意,填写下表:(单位:元)
(Ⅱ)分别就两家商场的让利方式,写出y关于x的函数解析式;
(Ⅲ)春节期间,当在同一商场累计购物超过200元时,哪家商场的实际花费少?
设x(单位:元)表示商品原价,y(单位:元)表示购物金额.
(Ⅰ)根据题意,填写下表:(单位:元)
| 商品价格 购物金额 | 120 | 180 | 200 | 260 |
| 甲商场 | 96 | 144 | 160 | 208 |
| 乙商场 | 120 | 200 | 200 | ,242 |
(Ⅲ)春节期间,当在同一商场累计购物超过200元时,哪家商场的实际花费少?
7.近几年,全社会对空气污染问题越来越重视,空气净化器的销量也在逐年增加.某商场从厂家购进了A、B两种型号的空气净化器,两种净化器的销售相关信息见下表:
(1)每台A型空气净化器和B型空气净化器的销售利润分别是多少?
(2)该公司计划一次购进两种型号的空气净化器共100台,其中B型空气净化器的进货量不少于A型空气净化器的2倍,为使该公司销售完这100台空气净化器后的总利润最大,请你设计相应的进货方案;
(3)已知A型空气净化器的净化能力为300m3/小时,B型空气净化器的净化能力为200m3/小时,某长方体室内活动场地的总面积为200m2,室内墙高3m,该场地负责人计划购买5台空气净化器每天花费30分钟将室内就欧诺个气净化一新,若不考虑空气对流等因素,至少要购买A型空气净化器多少台?
| A型销售数量(台) | B型销售数量(台) | 总利润(元) |
| 5 | 10 | 2000 |
| 10 | 5 | 2500 |
(2)该公司计划一次购进两种型号的空气净化器共100台,其中B型空气净化器的进货量不少于A型空气净化器的2倍,为使该公司销售完这100台空气净化器后的总利润最大,请你设计相应的进货方案;
(3)已知A型空气净化器的净化能力为300m3/小时,B型空气净化器的净化能力为200m3/小时,某长方体室内活动场地的总面积为200m2,室内墙高3m,该场地负责人计划购买5台空气净化器每天花费30分钟将室内就欧诺个气净化一新,若不考虑空气对流等因素,至少要购买A型空气净化器多少台?
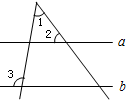 如图,直线a∥b,若∠1=55°,∠2=60°,则∠3=115°.
如图,直线a∥b,若∠1=55°,∠2=60°,则∠3=115°.