题目内容
4.(1)已知:如图①,在△ABC中,AB=AC=5,BC=6,点D在BC上,若线段AD平分△ABC的面积,请画出线段AD,并计算AD=4.(2)如图②,四边形ABCD是平行四边形(AB<BC),请你画一条直线l,使其平分?ABCD的面积,且直线l在?ABCD内部的线段最短,并说明理由.
(3)如图③,在四边形ABCD中,AD∥BC,AB>CD,是否存在过点A的一条直线将四边形ABCD的面积平分?如果存在,请画出符合条件的直线,并说明你的做法和理由,如果不存在,也请说明理由.

分析 (1)作中线AD,利用等腰三角形三线合一的性质和勾股定理求AD的长;
(2)经过平行四边形对角线中点的直线将平行四边形的面积分成相等的两部分,当MN⊥BC时,最短;
(3)取CD 的中点M,连接AM并延长交BC的延长线于N,取BN的中点E,则A,E的直线将四边形ABCD的面积平分,得到△ADM≌△CMN,于是得到S四边形AECD=S△AEN,等量代换得到结论.
解答 解:(1)如图①,作中线AD,则AD平分△ABC的面积,
∴BD=CD=$\frac{1}{2}$×6=3,
∵AC=AB=5,
∴AD⊥BC,
由勾股定理得:AD=$\sqrt{{5}^{2}-{3}^{2}}$=4;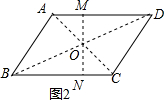
故答案为:4;
(2)连接AC、BD,交于O,
过O作直线MN,交AD于M,交BC于N,当MN⊥BC时,MN是最短,如图②,
∵四边形ABCD为平行四边形,
∴OA=OC,AD∥BC,
∴∠CAD=∠ACB,
∵∠AOM=∠CON,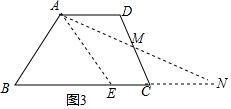
∴△AOM≌△CON,
∴S△AOM=S△CON,
同理可得:△OMD≌△ONB,△AOB≌△COD,
∴S△OMD=S△ONB,S△AOB=S△COD,
∴S△AOM+S△AOB+S△BON=S△CON+S△COD+S△OMD,
即MN将四边形ABCD分成面积相等的两部分;
(3)取CD 的中点M,连接AM并延长交BC的延长线于N,
取BN的中点E,则A,E的直线将四边形ABCD的面积平分,
理由:∵AD∥BC,
∴∠DAM=∠N,
在△ADM与△NCM中,$\left\{\begin{array}{l}{∠DAM=∠N}\\{∠AMD=∠CMN}\\{DM=CM}\end{array}\right.$,
∴△ADM≌△CMN,
∴S四边形AECD=S△AEN,
∵E是BN的中点,
∴S△ABE=S△AEN,
∴S四边形AECD=S△ABE.
点评 本题是四边形的综合题,考查了平行四边形、等腰三角形、梯形的性质,明确三角形的中线将三角形分成面积相等的两部分,过平行四边形对角线中点的直线将平行四边形的面积分成相等的两部分.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案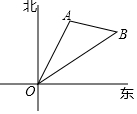 如图,海岛A在灯塔O处北偏东25°,海岛B在灯塔O处北偏东55°,海岛A在海岛B的北偏西80°,已知海岛A到灯塔的距离为80海里,求海岛B到灯塔的距离.(结果保留根号)
如图,海岛A在灯塔O处北偏东25°,海岛B在灯塔O处北偏东55°,海岛A在海岛B的北偏西80°,已知海岛A到灯塔的距离为80海里,求海岛B到灯塔的距离.(结果保留根号)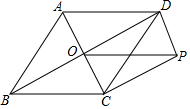 如图,在菱形ABCD中,AC、BD交于点O,BD=8,AC=4,DP∥AC,CP∥BD.
如图,在菱形ABCD中,AC、BD交于点O,BD=8,AC=4,DP∥AC,CP∥BD.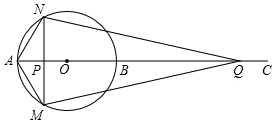 如图,AB为⊙O的直径,点C为AB延长线上一点,动点P从点A出发沿AC方向以1cm/s的速度运动,同时动点Q从点C出发以相同的速度沿CA方向运动,当两点相遇时停止运动,过点P作AB的垂线,分别交⊙O于点M和点N,已知⊙O的半径为$\frac{3}{2}$cm,AC=8cm,设运动时间为t秒.
如图,AB为⊙O的直径,点C为AB延长线上一点,动点P从点A出发沿AC方向以1cm/s的速度运动,同时动点Q从点C出发以相同的速度沿CA方向运动,当两点相遇时停止运动,过点P作AB的垂线,分别交⊙O于点M和点N,已知⊙O的半径为$\frac{3}{2}$cm,AC=8cm,设运动时间为t秒. 二次函数y=ax2+bx+c(a≠0)的图象如图所示,则抛物线与x轴的另一个交点坐标为(4,0).
二次函数y=ax2+bx+c(a≠0)的图象如图所示,则抛物线与x轴的另一个交点坐标为(4,0). 如图,平行四边形ABCD对角线相交于点O,M是AD的中点,连结CM,交BD于点N.则S△AOB:S△CON:S△DMN=3:1:1.
如图,平行四边形ABCD对角线相交于点O,M是AD的中点,连结CM,交BD于点N.则S△AOB:S△CON:S△DMN=3:1:1.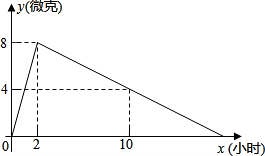 某医药研究所开发了一种新药,在试验药效时发现,如果成人按规定剂量服用,那么服药后2小时时血液中含药量最高,达每毫升6微克(1微克=10-3毫克),接着逐步衰减,10小时时血液中含药量为每毫升3微克,每毫升血液中含药量y(微克),随时间x(小时)的变化如图所示,当成人按规定剂量服药后,
某医药研究所开发了一种新药,在试验药效时发现,如果成人按规定剂量服用,那么服药后2小时时血液中含药量最高,达每毫升6微克(1微克=10-3毫克),接着逐步衰减,10小时时血液中含药量为每毫升3微克,每毫升血液中含药量y(微克),随时间x(小时)的变化如图所示,当成人按规定剂量服药后,