题目内容
10.甲乙两家商场平时以同样的价格出售相同的商品.春节期间两家商场都让利酬宾,其中甲商场所有商品按8折出售,乙商场对一次购物中超过200元后的价格部分打7折.设x(单位:元)表示商品原价,y(单位:元)表示购物金额.
(Ⅰ)根据题意,填写下表:(单位:元)
| 商品价格 购物金额 | 120 | 180 | 200 | 260 |
| 甲商场 | 96 | 144 | 160 | 208 |
| 乙商场 | 120 | 200 | 200 | ,242 |
(Ⅲ)春节期间,当在同一商场累计购物超过200元时,哪家商场的实际花费少?
分析 (Ⅰ)根据两家商场的让利方式分别列式整理即可;
(Ⅱ)甲商场按原价直接乘以0.8,乙商场分0≤x≤200、x>200两种情况分别列式即可;
(Ⅲ)求出两家商场购物付款相同的x的值,然后作出判断即可.
解答 解:(Ⅰ)
| 120 | 180 | 200 | 260 | |
| 甲商场 | 96 | 144 | 160 | 208 |
| 乙商场 | 120 | 180 | 200 | 242 |
(Ⅱ)甲商场:y=0.8x(x≥0);
乙商场:当0≤x≤200时,y=x;
当x>200时,y=200+0.7(x-200)=0.7x+60;
即y=$\left\{\begin{array}{l}{0≤x≤200}\\{x>200}\end{array}\right.$;
(Ⅲ)∵x≥200,
∴由0.8x=0.7x+60,得:x=600,
∴当购物金额按原价大于200而小于600元时,在甲商场购物省钱;
当购物金额按原价大于600元时,在两商场花钱一样多;
当购物金额按原价大于600元时,在乙商场购物省钱.
点评 本题考查了一次函数的应用,读懂题目信息,理解两家商场的让利方法是解题的关键,要注意乙商场根据商品原价的取值范围分情况讨论.

练习册系列答案
相关题目
11. 如图,△ABC 中,AB=AC,以AB为直径的⊙O与BC相交于点D,与CA的延长线相交于点E,过点D作DF⊥AC于点F.
如图,△ABC 中,AB=AC,以AB为直径的⊙O与BC相交于点D,与CA的延长线相交于点E,过点D作DF⊥AC于点F.
(1)求证:DF是⊙O的切线;
(2)若AC=3AE,写出求tanC的思路.
 如图,△ABC 中,AB=AC,以AB为直径的⊙O与BC相交于点D,与CA的延长线相交于点E,过点D作DF⊥AC于点F.
如图,△ABC 中,AB=AC,以AB为直径的⊙O与BC相交于点D,与CA的延长线相交于点E,过点D作DF⊥AC于点F.(1)求证:DF是⊙O的切线;
(2)若AC=3AE,写出求tanC的思路.
20.阅读下列材料,完成相应任务:
学习任务:
(1)将剩余部分的证明过程补充完整;
(2)若将图(1)中的点S与点D重合,重复材料中的操作过程得到图(4),请利用图(4),直接写出tan15°=2-$\sqrt{3}$(不必化简)
| 折纸三等分角 三等分角问题(trisection of an angle)是二千四百年前,古希腊人提出的几何三大作图问题之一(三等分任意角、化圆为方、倍立方),即用圆规与直尺(没有刻度,只能做直线的尺子)把一任意角三等分,这问题曾吸引着许多人去研究,但无一成功.1837年法国数学家凡齐尔(1814~1848)运用代数方法证明了,仅用尺规不可鞥呢三等分角. 如果作图工具没有限制,将条件放宽,将任意角三等分是可以解决的.下面介绍一种折纸三等分任意锐角的方法: (1)在正方形纸片上折出任意∠SBC,将正方形ABCD对折,折痕为记为MN,再将矩形MBCN对折,折痕记为EF,得到图(1); (2)翻折左下角使点B与EF上的点T重合,点M与SB上的点P重合,点E对折后的对应点记为Q,折痕为记为GH,得到图(2); (3)折出射线BQ,BT,得到图(3),则射线BQ,BT就是∠SBC的三等分线.  下面是证明BQ,BT是∠SBC三等分线的部分过程: 证明:过T作TK⊥BC,垂足为K,则四边形EBKT为矩形 根据折叠,得EB=QT,∠EBT=∠QTB,BT=TB ∴△EBT≌△QTB, ∴∠BQT=∠TEB=90°, ∴BQ⊥PT … |
(1)将剩余部分的证明过程补充完整;
(2)若将图(1)中的点S与点D重合,重复材料中的操作过程得到图(4),请利用图(4),直接写出tan15°=2-$\sqrt{3}$(不必化简)
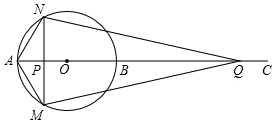 如图,AB为⊙O的直径,点C为AB延长线上一点,动点P从点A出发沿AC方向以1cm/s的速度运动,同时动点Q从点C出发以相同的速度沿CA方向运动,当两点相遇时停止运动,过点P作AB的垂线,分别交⊙O于点M和点N,已知⊙O的半径为$\frac{3}{2}$cm,AC=8cm,设运动时间为t秒.
如图,AB为⊙O的直径,点C为AB延长线上一点,动点P从点A出发沿AC方向以1cm/s的速度运动,同时动点Q从点C出发以相同的速度沿CA方向运动,当两点相遇时停止运动,过点P作AB的垂线,分别交⊙O于点M和点N,已知⊙O的半径为$\frac{3}{2}$cm,AC=8cm,设运动时间为t秒. 如图,平行四边形ABCD对角线相交于点O,M是AD的中点,连结CM,交BD于点N.则S△AOB:S△CON:S△DMN=3:1:1.
如图,平行四边形ABCD对角线相交于点O,M是AD的中点,连结CM,交BD于点N.则S△AOB:S△CON:S△DMN=3:1:1.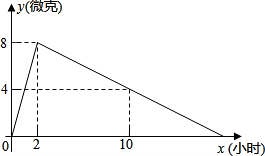 某医药研究所开发了一种新药,在试验药效时发现,如果成人按规定剂量服用,那么服药后2小时时血液中含药量最高,达每毫升6微克(1微克=10-3毫克),接着逐步衰减,10小时时血液中含药量为每毫升3微克,每毫升血液中含药量y(微克),随时间x(小时)的变化如图所示,当成人按规定剂量服药后,
某医药研究所开发了一种新药,在试验药效时发现,如果成人按规定剂量服用,那么服药后2小时时血液中含药量最高,达每毫升6微克(1微克=10-3毫克),接着逐步衰减,10小时时血液中含药量为每毫升3微克,每毫升血液中含药量y(微克),随时间x(小时)的变化如图所示,当成人按规定剂量服药后,