题目内容
11.下列分式中,最简分式是( )| A. | $\frac{{x}^{2}+{y}^{2}}{x+y}$ | B. | $\frac{a-b}{b-a}$ | C. | $\frac{{x}^{2}-4}{x-2}$ | D. | $\frac{2+a}{-4-4a-{a}^{2}}$ |
分析 要判断分式是否是最简分式,只需判断它能否化简,不能化简的即为最简分式.
解答 解:A、$\frac{{x}^{2}+{y}^{2}}{x+y}$不能约分,是最简分式;
B、$\frac{a-b}{b-a}$=-1;
C、$\frac{{x}^{2}-4}{x-2}$=x+2;
D、$\frac{2+a}{-4-4a-{a}^{2}}$=-$\frac{1}{a+2}$.
故选:A.
点评 此题考查了最简分式的判断,当分式的分子分母中除1以外再没有其他的公因式时,此时分式成为最简分式,一般情况下分式若不是最简分式,应将分子分母中的公因式约分后得到最简结果.掌握最简分式的判断方法是解本题的关键.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
1.已知关于x的方程kx2+(k+1)x+$\frac{k}{4}$=0有两个不相等的实数根,则k的取值范围( )
| A. | k=-$\frac{1}{2}$ | B. | k<-$\frac{1}{2}$ | C. | k≤-$\frac{1}{2}$ | D. | k>-$\frac{1}{2}$且k≠0 |
19. 如图所示,直线a∥b,∠B=16°,∠C=50°,则∠A的度数为( )
如图所示,直线a∥b,∠B=16°,∠C=50°,则∠A的度数为( )
 如图所示,直线a∥b,∠B=16°,∠C=50°,则∠A的度数为( )
如图所示,直线a∥b,∠B=16°,∠C=50°,则∠A的度数为( )| A. | 24° | B. | 26° | C. | 34° | D. | 36° |
 如图,在△ABC中,AB=AC,DE垂直平分AB交AC于点E,已知△BCE的周长为8,且AC-BC=2,求AB,BC的长.
如图,在△ABC中,AB=AC,DE垂直平分AB交AC于点E,已知△BCE的周长为8,且AC-BC=2,求AB,BC的长.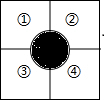 如图,一方形花坛分成编号为①、②、③、④四块,现有红、黄、蓝、紫四种颜色的花供选种.要求每块只种一种颜色的花,且相邻的两块种不同颜色的花,如果编号为①的已经种上红色花,那么其余三块不同的种法有( )种.
如图,一方形花坛分成编号为①、②、③、④四块,现有红、黄、蓝、紫四种颜色的花供选种.要求每块只种一种颜色的花,且相邻的两块种不同颜色的花,如果编号为①的已经种上红色花,那么其余三块不同的种法有( )种.