题目内容
6.下列命题:①若a+b+c=0,则b2-4ac<0;
②若b=2a+3c,则一元二次方程ax2+bx+c=0有两个不相等的实数根;
③若b>a+c,则一元二次方程ax2+bx+c=0有两个不相等的实数根;
④若b2-4ac>0,则二次函数y=ax2+bx+c的图象与坐标轴的公共点的个数是2或3;
⑤若ac+b+1=0,则二次函数y=ax2+bx+c的图象与x轴一定有交点.
其中正确的是②④⑤.
分析 把b=-(a+c)代入△=b2-4ac中计算可得△=(a-c)2,则可对①进行判断;把b=2a+3c代入△=b2-4ac中,利用配方法得到△=4(a+c)2+5c2,则可对②进行判断;利用反例对③进行判断;根据二次函数图象与x轴的交点问题可对④进行判断;先计算出△=(ac-1)2≥0,则根据二次函数图象与x轴的交点问题可对⑤进行判断.
解答 解:当b=-(a+c),△=b2-4ac=(a+c)2-4ac=(a-c)2≥0,所以①错误;
当b=2a+3c,△=b2-4ac=(2a+3c)2-4ac=4a2+8ac+9c2=4(a+c)2+5c2>0,所以②正确;
当b=0,a=-1,c=0,满足b>a+c,而此时方程为-x2=0,方程有两个相等的实数解,所以③错误;
若b2-4ac>0,二次函数y=ax2+bx+c的图象与x轴有两个公共点,当c=0时,抛物线过原点,此时抛物线与坐标轴有两个公共点;当c≠0,此时抛物线与坐标轴有三个公共点,所以④正确;
若b=-ac-1,△=b2-4ac=(-ac-1)2-4ac=(ac-1)2≥0,则二次函数y=ax2+bx+c的图象与x轴一定有交点,所以⑤正确.
故答案为②④⑤.
点评 本题考查了命题与定理:判断一件事情的语句,叫做命题.许多命题都是由题设和结论两部分组成,题设是已知事项,结论是由已知事项推出的事项,一个命题可以写成“如果…那么…”形式. 2、有些命题的正确性是用推理证实的,这样的真命题叫做定理.也考查了根的判别式和二次函数与x轴的交点问题.

练习册系列答案
相关题目
11.下列分式中,最简分式是( )
| A. | $\frac{{x}^{2}+{y}^{2}}{x+y}$ | B. | $\frac{a-b}{b-a}$ | C. | $\frac{{x}^{2}-4}{x-2}$ | D. | $\frac{2+a}{-4-4a-{a}^{2}}$ |
18.设甲数为a,乙数为b,甲乙两数的平方和与甲乙两数积的商的代数式是( )
| A. | $\frac{{a}^{2}+{b}^{2}}{ab}$ | B. | (a+b)2ab | C. | (a2+b2)$\frac{a}{b}$ | D. | $\frac{(a+b)^{2}}{ab}$ |
16.已知三角形三边长分别为3,x,14,若x为正整数,则这样的三角形个数为( )
| A. | 2 | B. | 3 | C. | 5 | D. | 13 |
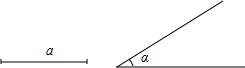 已知一直角边和这条直角边的对角,求作直角三角形(用尺规作图,不写作法,但要保留作图痕迹)
已知一直角边和这条直角边的对角,求作直角三角形(用尺规作图,不写作法,但要保留作图痕迹)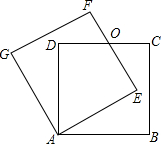 如图,正方形ABCD绕点A逆时针旋转n°后得到正方形AEFG,边EF与CD交于点O
如图,正方形ABCD绕点A逆时针旋转n°后得到正方形AEFG,边EF与CD交于点O