题目内容
2. 如图,在△ABC中,AB=AC,DE垂直平分AB交AC于点E,已知△BCE的周长为8,且AC-BC=2,求AB,BC的长.
如图,在△ABC中,AB=AC,DE垂直平分AB交AC于点E,已知△BCE的周长为8,且AC-BC=2,求AB,BC的长.
分析 根据线段的垂直平分线的性质得到EA=EB,根据△BCE的周长为8,求出AB,BC的长.
解答 解:∵DE垂直平分AB,
∴EA=EB,
△BCE的周长为8,即BC+CE+BE=8,
∴AC+BC=8,又AC-BC=2,
解得AC=5,BC=3.
点评 此题主要考查线段的垂直平分线的性质,掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键.

练习册系列答案
相关题目
13.下列式子正确的是( )
| A. | (x-y)2=x2-xy+y2 | B. | -x(x2-x+1)=-x3-x2-x | ||
| C. | (2ab2)3=6a3b6 | D. | 9x3y2÷(-3x3y)=-3y |
11.下列分式中,最简分式是( )
| A. | $\frac{{x}^{2}+{y}^{2}}{x+y}$ | B. | $\frac{a-b}{b-a}$ | C. | $\frac{{x}^{2}-4}{x-2}$ | D. | $\frac{2+a}{-4-4a-{a}^{2}}$ |
12.在△ABC中,∠C=90°,AB=10,cosA=$\frac{4}{5}$,则BC的长为( )
| A. | 6 | B. | 7.5 | C. | 8 | D. | 12.5 |
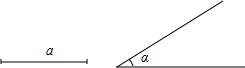 已知一直角边和这条直角边的对角,求作直角三角形(用尺规作图,不写作法,但要保留作图痕迹)
已知一直角边和这条直角边的对角,求作直角三角形(用尺规作图,不写作法,但要保留作图痕迹)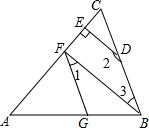 已知:如图,∠AGF=∠ABC,∠1+∠2=180°,DE⊥AC于点E.
已知:如图,∠AGF=∠ABC,∠1+∠2=180°,DE⊥AC于点E.