题目内容
13.先化简,再求值:($\frac{1}{x-y}$-$\frac{1}{{x}^{2}-xy}$)÷$\frac{x-2}{3x}$,其中x=2+tan60°,y=4sin30°.
分析 根据分式的混合运算法则把分式化简,根据特殊角的三角函数值把x、y化简,代入化简后的分式,根据二次根式的混合运算法则计算即可.
解答 解:原式=[$\frac{x}{x(x-y)}$-$\frac{1}{x(x-y)}$]×$\frac{3x}{x-2}$
=$\frac{3x(x-1)}{x(x-y)(x-2)}$
=$\frac{3(x-1)}{(x-y)(x-2)}$,
当x=2+tan60°=2+$\sqrt{3}$,y=4sin30°=2时,
原式=$\frac{3×(\sqrt{3}+1)}{(\sqrt{3}+2-2)(\sqrt{3}+2-2)}$=$\sqrt{3}$+1.
点评 本题考查的是分式的化简求值、二次根式的计算以及特殊角的三角函数值,在化简的过程中要注意运算顺序和分式的化简.化简的最后结果分子、分母要进行约分,注意运算的结果要化成最简分式或整式.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
2.设a,b是方程x2+x-2016=0的两个实数根,则a2+2a+b的值为( )
| A. | 2014 | B. | 2015 | C. | 2016 | D. | 2017 |
16.在坐标系中,已知A(2,0),B(-3,-4),C(0,0),则△ABC的面积为( )
| A. | 4 | B. | 6 | C. | 8 | D. | 3 |
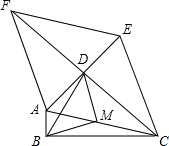 定义:只有一组对角是直角的四边形叫做损矩形,连接它的两个非直角顶点的线段叫做这个矩形的直径.如图,△ABC中.∠ABC=90°,以AC为一边向形外作菱形ACEF,点D是菱形ACEF对角线的交点,可以得到损矩形ABCD,连接BD,则有∠DBC=∠DAC,∠DBC=60°,∠ACB=15°
定义:只有一组对角是直角的四边形叫做损矩形,连接它的两个非直角顶点的线段叫做这个矩形的直径.如图,△ABC中.∠ABC=90°,以AC为一边向形外作菱形ACEF,点D是菱形ACEF对角线的交点,可以得到损矩形ABCD,连接BD,则有∠DBC=∠DAC,∠DBC=60°,∠ACB=15° 如图,已知AB∥CD,∠BAE=3∠ECF,∠ECF=28°,求∠E的度数.
如图,已知AB∥CD,∠BAE=3∠ECF,∠ECF=28°,求∠E的度数.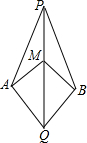 如图,已知PA=PB,QA=QB,求证:MA=MB.
如图,已知PA=PB,QA=QB,求证:MA=MB.