题目内容
1.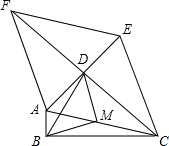 定义:只有一组对角是直角的四边形叫做损矩形,连接它的两个非直角顶点的线段叫做这个矩形的直径.如图,△ABC中.∠ABC=90°,以AC为一边向形外作菱形ACEF,点D是菱形ACEF对角线的交点,可以得到损矩形ABCD,连接BD,则有∠DBC=∠DAC,∠DBC=60°,∠ACB=15°
定义:只有一组对角是直角的四边形叫做损矩形,连接它的两个非直角顶点的线段叫做这个矩形的直径.如图,△ABC中.∠ABC=90°,以AC为一边向形外作菱形ACEF,点D是菱形ACEF对角线的交点,可以得到损矩形ABCD,连接BD,则有∠DBC=∠DAC,∠DBC=60°,∠ACB=15°(1)点M是AC中点,连接BM,DM,判断△MBD的形状,并说明理由.
(2)若BD=2$\sqrt{3}$,求:菱形ACEF的面积.
分析 (1)由菱形的性质得出AE⊥CF,AD=$\frac{1}{2}$AE,CD=$\frac{1}{2}$CF,由直角三角形斜边上的中线性质得出DM=BM=CM,得出∠BDM=∠DBM,∠MBC=∠ACB=15°,求出∠DBM=∠BDM=45°,证出∠BMD=90°即可;
(2)由等腰直角三角形的性质和勾股定理得出BM=$\frac{\sqrt{2}}{2}$BD=$\sqrt{6}$,得出AC=2$\sqrt{6}$,由含30°角的直角三角形的性质得出AD=$\frac{1}{2}$AC=$\sqrt{6}$,得出CD=3$\sqrt{2}$,求出AE=2AD=2$\sqrt{6}$,CF=2CD=6$\sqrt{2}$,即可得出结果.
解答 解:(1)△MBD是等腰直角三角形;理由如下:
∵四边形ACEF是菱形,
∴AE⊥CF,AD=$\frac{1}{2}$AE,CD=$\frac{1}{2}$CF,
∴∠ADC=90°=∠ABC,
∵点M是AC中点,
∴DM=$\frac{1}{2}$AC=AM=CM,BM=$\frac{1}{2}$AC=CM,
∴DM=BM=CM,
∴∠BDM=∠DBM,∠MBC=∠ACB=15°,
∵∠DBC=60°,
∴∠DBM=∠BDM=60°-15°=45°,
∴∠BMD=90°,
∴△MBD是等腰直角三角形;
(2)由(1)得:△MBD是等腰直角三角形,
∴BM=$\frac{\sqrt{2}}{2}$BD=$\sqrt{6}$,
∴AC=2$\sqrt{6}$,
∵∠DBC=∠DAC=60°,
∴∠ACD=90°-60°=30°,
∴AD=$\frac{1}{2}$AC=$\sqrt{6}$,CD=$\sqrt{3}$AD=$\sqrt{3}$×$\sqrt{6}$=3$\sqrt{2}$,
∴AE=2AD=2$\sqrt{6}$,CF=2CD=6$\sqrt{2}$,
∴菱形ACEF的面积=$\frac{1}{2}$×2$\sqrt{6}$×6$\sqrt{2}$=12$\sqrt{3}$.
点评 本题考查了菱形的性质、直角三角形斜边上的中线性质、等腰直角三角形的判定与性质、勾股定理等知识;熟练掌握菱形的性质,证明三角形是等腰直角三角形是解决问题的关键.

| A. | (a+b)2=a2+b2 | B. | (ab)2=ab2 | C. | a•a2=a3 | D. | (a3)2=a5 |
 如图,AB∥DE,AC⊥CD,并且∠A=35°,则∠D的度数为( )
如图,AB∥DE,AC⊥CD,并且∠A=35°,则∠D的度数为( )| A. | 55° | B. | 45° | C. | 30° | D. | 60° |
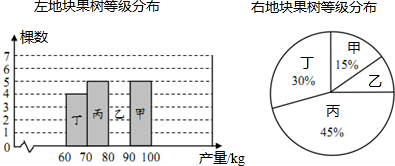
 一个由若干个相同的正方体组成的几何体,其主视图和左视图如图所示,这个几何体最少可以由10个这样的正方体组成.
一个由若干个相同的正方体组成的几何体,其主视图和左视图如图所示,这个几何体最少可以由10个这样的正方体组成.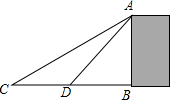 天下第一门-华门,位于山西省临汾市尧都区尧庙广场的西面,是一座纪念华夏文明的门.周日,小韬与同学一起来到华门前游玩,他想通过测量来计算华门的高度,于是他借来测角仪和卷尺,如图,他在点C处测得华门AB顶端A的仰角为30°,沿着CB方向向华门行进了36.6米到达点D处,测得华门AB顶端A的仰角为45°,求华门AB的高为多少?(结果保留整数,参考数据$\sqrt{3}$≈1.73)
天下第一门-华门,位于山西省临汾市尧都区尧庙广场的西面,是一座纪念华夏文明的门.周日,小韬与同学一起来到华门前游玩,他想通过测量来计算华门的高度,于是他借来测角仪和卷尺,如图,他在点C处测得华门AB顶端A的仰角为30°,沿着CB方向向华门行进了36.6米到达点D处,测得华门AB顶端A的仰角为45°,求华门AB的高为多少?(结果保留整数,参考数据$\sqrt{3}$≈1.73)