题目内容
2．设a，b是方程x2+x-2016=0的两个实数根，则a2+2a+b的值为（ ）| A． | 2014 | B． | 2015 | C． | 2016 | D． | 2017 |
分析 先根据一元二次方程的解的定义得到a2+a-2016=0，即a2=-a+2016，则a2+2a+b可化简为a+b+2016，再根据根与系数的关系得a+b=-1，然后利用整体代入的方法计算．
解答 解：∵a是方程x2+x-2016=0的实数根，
∴a2+a-2016=0，
∴a2=-a+2016，
∴a2+2a+b=-a+2016+2a+b=a+b+2016，
∵a、b是方程x2+x-2016=0的两个实数根，
∴a+b=-1，
∴a2+2a+b=-1+2016=2015．
故选B．
点评 本题考查了根与系数的关系：若x1，x2是一元二次方程ax2+bx+c=0（a≠0）的两根时，x1+x2=-$\frac{b}{a}$，x1x2=$\frac{c}{a}$．也考查了一元二次方程的解．
练习册系列答案
相关题目
12．下列计算正确的是（ ）
| A． | （a+b）2=a2+b2 | B． | （ab）2=ab2 | C． | a•a2=a3 | D． | （a3）2=a5 |
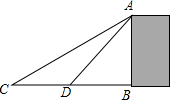天下第一门-华门，位于山西省临汾市尧都区尧庙广场的西面，是一座纪念华夏文明的门．周日，小韬与同学一起来到华门前游玩，他想通过测量来计算华门的高度，于是他借来测角仪和卷尺，如图，他在点C处测得华门AB顶端A的仰角为30°，沿着CB方向向华门行进了36.6米到达点D处，测得华门AB顶端A的仰角为45°，求华门AB的高为多少？（结果保留整数，参考数据$\sqrt{3}$≈1.73）