题目内容
4.(1)解方程:x2+x-1=0(2)抛物线y=-x2+bx+c经过点(1,0),(-3,0),求b、c的值.
分析 (1)求出根的判别式,利用公式法求出方程的解;
(2)利用待定系数法列出b和c的二元一次方程组,求出b和c的值即可.
解答 解:(1)a=1,b=1,c=-1,
△=b2-4ac=5,
则x=$\frac{-1±\sqrt{5}}{2×1}$,
x1=$\frac{-1+\sqrt{5}}{2}$,x2=$\frac{-1-\sqrt{5}}{2}$;
(2)∵y=-x2+bx+c经过点(1,0),(-3,0),
∴$\left\{\begin{array}{l}{-1+b+c=0}\\{-9-3b+c=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{b=-2}\\{c=3}\end{array}\right.$.
点评 本题主要考查了抛物线与x轴的交点以及用公式法解一元二次方程的知识,解题的关键是掌握待定系数法求出函数的解析式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19. 如图,菱形ABCD的周长为8,高AE长为$\sqrt{3}$,则AC:BD=( )
如图,菱形ABCD的周长为8,高AE长为$\sqrt{3}$,则AC:BD=( )
 如图,菱形ABCD的周长为8,高AE长为$\sqrt{3}$,则AC:BD=( )
如图,菱形ABCD的周长为8,高AE长为$\sqrt{3}$,则AC:BD=( )| A. | 1:2 | B. | 1:3 | C. | 1:$\sqrt{2}$ | D. | 1:$\sqrt{3}$ |
16.已知a=$\frac{4}{9}$m-1,b=m2-$\frac{5}{9}$m(m为任意实数),则a与b的大小关系为( )
| A. | a>b | B. | a<b | C. | a=b | D. | 不能确定 |
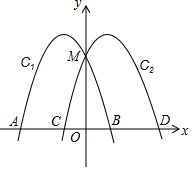 如图,抛物线C:y=-x2-2x+3交x轴于A、B两点,交y轴于M点,将抛物线C1向右平移2个单位后得到抛物线C2,与x轴交于C、D两点.
如图,抛物线C:y=-x2-2x+3交x轴于A、B两点,交y轴于M点,将抛物线C1向右平移2个单位后得到抛物线C2,与x轴交于C、D两点.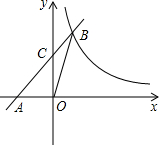 如图,在平面直角坐标系中,直线y=x+2与x轴交于点A,与y轴交于点C,与反比例函数y=$\frac{3}{x}$在第一象限内的图象交于点B(1,3),连接BO,下面三个结论:①S△AOB=1.5,;②点(x1,y1)和点(x2,y2)在反比例函数的图象上,若x1>x2,则y1<y2;③不等式x+2<$\frac{3}{x}$的解集是0<x<1.其中正确的有( )
如图,在平面直角坐标系中,直线y=x+2与x轴交于点A,与y轴交于点C,与反比例函数y=$\frac{3}{x}$在第一象限内的图象交于点B(1,3),连接BO,下面三个结论:①S△AOB=1.5,;②点(x1,y1)和点(x2,y2)在反比例函数的图象上,若x1>x2,则y1<y2;③不等式x+2<$\frac{3}{x}$的解集是0<x<1.其中正确的有( )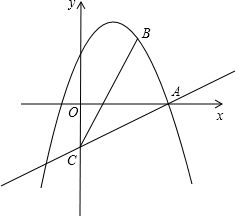 如图,在平面直角坐标系xOy中,抛物线y=-x2+bx+c经过点A(3,0)和点B(2,3),过点A的直线与y轴的负半轴相交于点C,且tan∠CAO=$\frac{1}{3}$.
如图,在平面直角坐标系xOy中,抛物线y=-x2+bx+c经过点A(3,0)和点B(2,3),过点A的直线与y轴的负半轴相交于点C,且tan∠CAO=$\frac{1}{3}$. 如图,AD是△ABC的角平分线,DF⊥AB,垂足为F,DE=DG,△ADG和△AED的面积分别为65和33,则△EDF的面积为16.
如图,AD是△ABC的角平分线,DF⊥AB,垂足为F,DE=DG,△ADG和△AED的面积分别为65和33,则△EDF的面积为16.