题目内容
15.在△ABC中,∠B=2∠C,AD为∠A的角平分线,mAB=nBD(n>m>0),则cosC=$\frac{m+n}{2n}$.分析 延长BK使BK=AB,过AH⊥BD于H,根据正弦定理和角平分线的定理以及余弦的定义即可求出cosC.
解答 解:如图 ,
,
延长BK使BK=AB,过AH⊥BD于H,
∵∠B=2∠C,
∴△ABK,△AKC为等腰三角形,
∴H为中点,
∵mAB=nBD,不妨设AB=n,BD=m,
则BH=ABcos2θ=mcos2θ
由正弦定理得$\frac{AB}{sinθ}$,
∴AC=2ncosθ
由角平分线定理知道CD=2mcosθ,
∵H是中点,
∴n+ncos2θ=$\frac{1}{2}$(m+2mcosθ),
即4ncos2θ-2mcosθ-(m+n)=0,
解得cosθ=$\frac{m+n}{2n}$,
故答案为:$\frac{m+n}{2n}$.
点评 本题考查了等腰三角形的判定和性质、正弦定理、角平分线定理以及三角形的外角和定理,题目的综合性较强,难度较大,正确的作出辅助线是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.相反数等于2的数是( )
| A. | 2 | B. | -2 | C. | ±2 | D. | $\frac{1}{2}$ |
7. 如图,直线AB与CD相交于点O,若∠1+∠2=80°,则∠3等于( )
如图,直线AB与CD相交于点O,若∠1+∠2=80°,则∠3等于( )
 如图,直线AB与CD相交于点O,若∠1+∠2=80°,则∠3等于( )
如图,直线AB与CD相交于点O,若∠1+∠2=80°,则∠3等于( )| A. | 100° | B. | 120° | C. | 140° | D. | 160° |
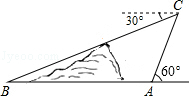 如图,在小山的东侧A点处有一个热气球,由于受西风的影响,以每分钟30米的速度沿与地面成60°角的方向飞行,20分钟后到达C处,此时热气球上的人测得小山西侧B点的俯角为30°,则A、B两点间的距离为600米.
如图,在小山的东侧A点处有一个热气球,由于受西风的影响,以每分钟30米的速度沿与地面成60°角的方向飞行,20分钟后到达C处,此时热气球上的人测得小山西侧B点的俯角为30°,则A、B两点间的距离为600米.