题目内容
19. 如图,菱形ABCD的周长为8,高AE长为$\sqrt{3}$,则AC:BD=( )
如图,菱形ABCD的周长为8,高AE长为$\sqrt{3}$,则AC:BD=( )| A. | 1:2 | B. | 1:3 | C. | 1:$\sqrt{2}$ | D. | 1:$\sqrt{3}$ |
分析 首先设设AC,BD相较于点O,由菱形ABCD的周长为8,可求得AB=BC=2,又由高AE长为$\sqrt{3}$,利用勾股定理即可求得BE的长,继而可得AE是BC的垂直平分线,则可求得AC的长,继而求得BD的长,则可求得答案.
解答 解:如图,设AC,BD相较于点O,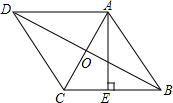
∵菱形ABCD的周长为8,
∴AB=BC=2,
∵高AE长为$\sqrt{3}$,
∴BE=$\sqrt{A{B}^{2}-A{E}^{2}}$=1,
∴CE=BE=1,
∴AC=AB=2,
∵OA=1cm,AC⊥BD,
∴OB=$\sqrt{A{B}^{2}-O{A}^{2}}$=$\sqrt{3}$,
∴BD=2OB=2$\sqrt{3}$,
∴AC:BD=1:$\sqrt{3}$.
故选D.
点评 此题考查了菱形的性质以及勾股定理.注意菱形的四条边都相等,对角线互相平分且垂直.

练习册系列答案
相关题目
7. 如图,直线AB与CD相交于点O,若∠1+∠2=80°,则∠3等于( )
如图,直线AB与CD相交于点O,若∠1+∠2=80°,则∠3等于( )
 如图,直线AB与CD相交于点O,若∠1+∠2=80°,则∠3等于( )
如图,直线AB与CD相交于点O,若∠1+∠2=80°,则∠3等于( )| A. | 100° | B. | 120° | C. | 140° | D. | 160° |
14.摩拜单车进入济南,为市民出行提供了极大方便,摩拜单车来济南第一个月的时间里,1.1万辆车被骑行了3280000人次,3280000用科学记数法表示为( )
| A. | 3.28×102 | B. | 32.8×105 | C. | 3.28×106 | D. | 3.28×107 |
9.生活中处处有数学,下列原理运用错误的是( )
| A. | 建筑工人砌墙时拉的参照线是运用“两点之间线段最短”的原理 | |
| B. | 修理损坏的椅子腿时斜钉的木条是运用“三角形稳定性”的原理 | |
| C. | 测量跳远的成绩是运用“垂线段最短”的原理 | |
| D. | 将车轮设计为圆形是运用了“圆的旋转对称性”原理 |
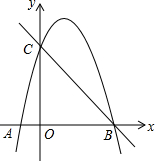 如图,抛物线y=ax2+3x+c经过A(-1,0),B(4,0)两点,与y轴交于点C
如图,抛物线y=ax2+3x+c经过A(-1,0),B(4,0)两点,与y轴交于点C 如图,点D是等边△ABC内一点,DA=8,BD=10,CD=6,则∠ADC的度数是150°.
如图,点D是等边△ABC内一点,DA=8,BD=10,CD=6,则∠ADC的度数是150°.