题目内容
12.小李创办了一家报刊零售点,对经营的某种晚报,他提供了如下信息:①买进每份0.20元,卖出0.30元;
②在一个月内(以30天计),其中有20天每天可以卖出200份,其余的10天每天就只能卖出120份;
③一个月内,每天从报社买进的报纸份数必须相同,当天卖不掉的报纸以每份0.10元退回给报社.
(1)第一个月为试营业阶段,他每天买进该晚报100份,这个月利润多少元?
(2)第二个月每天买进该晚报150份时,这个月利润多少元?
(3)设每天从报社买进晚报x份(120≤X≤200)时,月利润为y元,试写出y和x的函数关系式,并求出月利润的最大值.
分析 (1)当每天进报纸是100份时,根据有20天每天可以卖出200份,其余的10天每天就只能卖出120份可知道报纸都能卖出,从而求得利润;
(2)当进150份报纸时,有10天卖出120份,所以有剩下的报纸,再根据当天卖不掉的报纸以每份0.10元退回给报社可求出利润;
(3)设每天从报社买进晚报x份(120≤x≤200)时,利润y=20天全卖掉情况的利润+10天卖掉120份的利润-10天中每天卖不掉的报纸赔的钱,根据此关系式可列出函数式.
解答 解:(1)一个月每天买进该晚报的份数为100时:30×(0.30-0.20)×100=300(元);
(2)一个月每天买进该晚报的份数为150时:20×(0.30-0.20)×150+10×(0.30-0.20)×120-10×(0.20-0.10)×(150-120)=390(元);
(3)设每天从报社买进晚报x份(120≤x≤200且为整数)时,
y=20(0.30-0.20)x+10×(0.30-0.20)×120-10(x-120)(0.20-0.10)=x+240.
当x取最大值时,y取到最大值.
x的最大值为200,
∴y=200+240=440.
月利润的最大值为440.
点评 本题考查一次函数的应用,根据题意列出函数式,以及根据函数式的特点和自变量的取值范围求出最值.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
7. 如图,直线AB与CD相交于点O,若∠1+∠2=80°,则∠3等于( )
如图,直线AB与CD相交于点O,若∠1+∠2=80°,则∠3等于( )
 如图,直线AB与CD相交于点O,若∠1+∠2=80°,则∠3等于( )
如图,直线AB与CD相交于点O,若∠1+∠2=80°,则∠3等于( )| A. | 100° | B. | 120° | C. | 140° | D. | 160° |
2.|-6|=( )
| A. | $\frac{1}{6}$ | B. | 6 | C. | -6 | D. | ±6 |


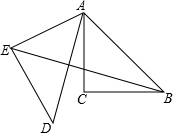 已知,在Rt△ABC中,∠C=90°,∠BAC=45°,AC=2,将△ABC绕点A顺时针旋转60°得到△ADE,连接BE,则BE的长为$\sqrt{2}+\sqrt{6}$.
已知,在Rt△ABC中,∠C=90°,∠BAC=45°,AC=2,将△ABC绕点A顺时针旋转60°得到△ADE,连接BE,则BE的长为$\sqrt{2}+\sqrt{6}$.