题目内容
9.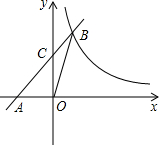 如图,在平面直角坐标系中,直线y=x+2与x轴交于点A,与y轴交于点C,与反比例函数y=$\frac{3}{x}$在第一象限内的图象交于点B(1,3),连接BO,下面三个结论:①S△AOB=1.5,;②点(x1,y1)和点(x2,y2)在反比例函数的图象上,若x1>x2,则y1<y2;③不等式x+2<$\frac{3}{x}$的解集是0<x<1.其中正确的有( )
如图,在平面直角坐标系中,直线y=x+2与x轴交于点A,与y轴交于点C,与反比例函数y=$\frac{3}{x}$在第一象限内的图象交于点B(1,3),连接BO,下面三个结论:①S△AOB=1.5,;②点(x1,y1)和点(x2,y2)在反比例函数的图象上,若x1>x2,则y1<y2;③不等式x+2<$\frac{3}{x}$的解集是0<x<1.其中正确的有( )| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
分析 ①将y=0代入y=x+2中求出x值,由此即可得出OA的长度,结合点B的纵坐标结合三角形的面积即可求出S△AOB=3,结论①不正确;②当x1>0>x2时,可得出y1>0>y2,结论②不正确;③联立两函数解析式成方程组,解方程组可得出两函数图象的交点坐标,根据两函数图象的上下位置关系结合图形即可得出不等式x+2<$\frac{3}{x}$的解集是x<-3或0<x<1,结论③不正确.综上即可得出结论.
解答 解:①当y=x+2=0时,x=-2,
∴点A(-2,0),
∴OA=2,
∴S△AOB=$\frac{1}{2}$OA•|yB|=$\frac{1}{2}$×2×3=3,结论①不正确;
②当x1>0>x2时,y1>0>y2,结论②不正确;
③联立两函数解析式成方程组,
$\left\{\begin{array}{l}{y=x+2}\\{y=\frac{3}{x}}\end{array}\right.$,解得:$\left\{\begin{array}{l}{{x}_{1}=-3}\\{{y}_{1}=-1}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=1}\\{{y}_{2}=3}\end{array}\right.$,
观察函数图象可知:当x<-3或0<x<1时,直线y=x+2在反比例函数y=$\frac{3}{x}$图象的下方,
∴不等式x+2<$\frac{3}{x}$的解集是x<-3或0<x<1,结论③不正确.
故选A.
点评 本题考查了反比例函数与一次函数的交点问题、一次函数图象上点的坐标特点、三角形的面积以及反比例函数的性质,逐一分析三条结论的正误是解题的关键.

练习册系列答案
相关题目
18.如图所示,在平面直角坐标系中A(0,0),B(2,0),△AP1B是等腰直角三角形,且∠P1=90°,把△AP1B绕点B顺时针旋转180°,得到△BP2C1;把△绕点C顺时针旋转180°,得到△CP2D.依此类推,则旋转第2016次后,得到的等腰直角三角形的直角顶点P2017的坐标为( )
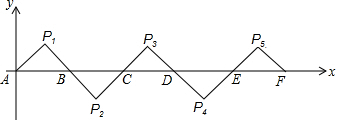

| A. | (4030,1) | B. | (4029,-1) | C. | (4033,1) | D. | (4031,-1) |

 【阅读新知】
【阅读新知】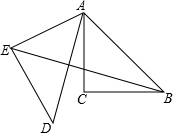 已知,在Rt△ABC中,∠C=90°,∠BAC=45°,AC=2,将△ABC绕点A顺时针旋转60°得到△ADE,连接BE,则BE的长为$\sqrt{2}+\sqrt{6}$.
已知,在Rt△ABC中,∠C=90°,∠BAC=45°,AC=2,将△ABC绕点A顺时针旋转60°得到△ADE,连接BE,则BE的长为$\sqrt{2}+\sqrt{6}$.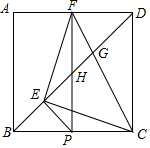 如图,正方形ABCD中,P为BC上一点,PE⊥BD于E,PF⊥AD于F,连接EF、CF.
如图,正方形ABCD中,P为BC上一点,PE⊥BD于E,PF⊥AD于F,连接EF、CF.