题目内容
14.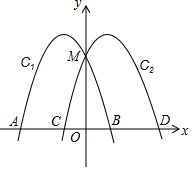 如图,抛物线C:y=-x2-2x+3交x轴于A、B两点,交y轴于M点,将抛物线C1向右平移2个单位后得到抛物线C2,与x轴交于C、D两点.
如图,抛物线C:y=-x2-2x+3交x轴于A、B两点,交y轴于M点,将抛物线C1向右平移2个单位后得到抛物线C2,与x轴交于C、D两点.(1)求抛物线C2对应的函数表达式;
(2)抛物线C1或C2在x轴上方的部分是否存在点N,使以A、C、M、N为顶点的四边形是平行四边形?若存在,求出点N的坐标,若不存在,请说明理由.
分析 (1)根据自变量与函数值的对应关系,可得A、B,根据平移规律,可得C,D,根据交点式函数解析式,可得答案;
(2)根据平移规律,可得MN与AC的关系,根据平行四边形的判定,可得答案.
解答 解:(1)当y=0时,-x2-2x+3=0,
解得x1=-3,x2=1,∴A(-3,0),B(1,0),
∵将抛物线C1向右平移2个单位后得到抛物线C2,
∴C(-1,0),D(3,0),a=-1,
∴抛物线C2对应的函数表达式y=-(x+1)(x-3),
即y=-x2+2x+3;
(2)存在,
如图1 ,
,
①令x=0,得y=3,∴M(0,3),
∵抛物线C2时C1向右平移2个单位得到的,
∴点N(2,3)在C2上,且MN=2,MN∥AC.
∵AC=2,
∴MN=AC,
∴四边形ACNM为平行四边形,
②令x=0,得y=3,
∴M(0,3),
∵抛物线C1向右平移2个单位得到C2,
∴点N(-2,3)在C2上,且MN′=2,MN′∥AC.
∵AC=2,
∴MN′=AC,
∴四边形ACMN′为平行四边形,
综上所述,存在点N(2,3)(-2,3),使得以A、C、M、N为顶点的四边形是平行四边形.
点评 本题考察了二次函数综合题,解(1)的关键是利用平移得出C,D点的坐标,又利用了交点式解析式;解(2)的关键是利用一组对边平行且相等的四边形是平行四边形,要分类讨论,以防遗漏.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目
6.相反数等于2的数是( )
| A. | 2 | B. | -2 | C. | ±2 | D. | $\frac{1}{2}$ |

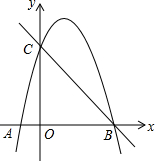 如图,抛物线y=ax2+3x+c经过A(-1,0),B(4,0)两点,与y轴交于点C
如图,抛物线y=ax2+3x+c经过A(-1,0),B(4,0)两点,与y轴交于点C