题目内容
已知抛物线y=x2-2x+a与直线y=x+1有两个公共点A(x1,y1),B(x2,y2),x2>x1≥0.
(1)求a的取值范围;
(2)作AE⊥x轴于点E,BF⊥x轴于点F,求四边形ABFE面积最大值.
(1)求a的取值范围;
(2)作AE⊥x轴于点E,BF⊥x轴于点F,求四边形ABFE面积最大值.
考点:二次函数的性质
专题:
分析:(1)联立直线和抛物线的解析式消去y得到的一元二次方程有两个不相等的实数根,利用判别式大于0可求得a的取值范围;
(2)利用(1)可表示出AE、BF、EF,表示出梯形ABFE的面积,再结合根与系数的关系得到关于a的函数,利用函数的增减性可求得其最大值.
(2)利用(1)可表示出AE、BF、EF,表示出梯形ABFE的面积,再结合根与系数的关系得到关于a的函数,利用函数的增减性可求得其最大值.
解答:解:(1)∵抛物线y=x2-2x+a与直线y=x+1相交∴x2-2x+ax+1 得x2-3x+a-1=0.
由题意可知x1,x2是方程x2-3x+a-1=0的两个不相等的根,
∴x1+x2=3,x1•x2=a-1,
∵x2>x1≥0,
∴x1•x2≥0,
得a-1≥0,a≥1,
又∵△=13-4a>0,
∴a<
,
故1≤a<
.
(2)∵A、B两点在直线y=x+1上,
∴y1=x1+1,y2=x2+1,
∴AE=x1+1,BF=x2+1,且OE=x1,OF=x2,
∴EF=x2-x1,
∴S四边形ABFE=
(AE+BF)EF=
(x1+1+x2+1)(x2-x1)=
(x22-x12)+(x2-x1),
又∵x1,x2是方程x2-3x+a-1=0的两根,
∴x12=3x1-a+1,x22=3x2-a+1,x1x2=a-1,x1+x2=3,
∴x22-x12=3(x2-x1),x2-x1=
=
∴S四边形ABFE=
(x2-x1)=
,
又∵1≤a<
,
∴a=1时,S梯形ABFE取最大值
.
由题意可知x1,x2是方程x2-3x+a-1=0的两个不相等的根,
∴x1+x2=3,x1•x2=a-1,
∵x2>x1≥0,
∴x1•x2≥0,
得a-1≥0,a≥1,
又∵△=13-4a>0,
∴a<
| 13 |
| 4 |
故1≤a<
| 13 |
| 4 |
(2)∵A、B两点在直线y=x+1上,
∴y1=x1+1,y2=x2+1,
∴AE=x1+1,BF=x2+1,且OE=x1,OF=x2,
∴EF=x2-x1,
∴S四边形ABFE=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
又∵x1,x2是方程x2-3x+a-1=0的两根,
∴x12=3x1-a+1,x22=3x2-a+1,x1x2=a-1,x1+x2=3,
∴x22-x12=3(x2-x1),x2-x1=
| (x1+x2)2-4x1x2 |
| 13-4a |
∴S四边形ABFE=
| 5 |
| 2 |
| 5 |
| 2 |
| 13-4a |
又∵1≤a<
| 13 |
| 4 |
∴a=1时,S梯形ABFE取最大值
| 15 |
| 2 |
点评:本题主要考查二次函数与一元二次方程的关系,在(2)中利用根与系数的关系用a表示出四边形的面积是解题的关键.

练习册系列答案
相关题目
若(x-4)0-(2x-6)-2有意义,则x的取值范围是( )
| A、x>4 |
| B、x<3 |
| C、x≠4或x≠3 |
| D、x≠4且x≠3 |


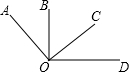 如图,∠AOC=∠BOD=90°,且∠DOC:∠BOC=2:7,求∠AOB,∠AOD的度数.
如图,∠AOC=∠BOD=90°,且∠DOC:∠BOC=2:7,求∠AOB,∠AOD的度数. 如图,△ABC绕点A旋转后能与△ADE重合,
如图,△ABC绕点A旋转后能与△ADE重合,