题目内容
在梯形ABCD中,AB∥CD,∠CAB=∠DBA.求证:梯形ABCD是等腰梯形.
考点:等腰梯形的判定
专题:证明题
分析:根据平行线的性质和已知求出∠CDO=∠DCO,求出OA=OB,OC=OD,证△DOA≌△COB,推出AD=BC,根据等腰梯形的判定得出即可.
解答: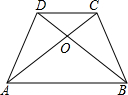 证明:∵AB∥CD,
证明:∵AB∥CD,
∴∠DCO=∠CAB,∠CDO=∠DBA,
∵∠CAB=∠DBA,
∴OA=OB,∠DCO=∠CDO,
∴OC=OD,
在△DOA和△COB中,
,
∴△DOA≌△COB(SAS),
∵AD=BC,
∵四边形ABCD是梯形,
∴四边形ABCD是等腰梯形.
 证明:∵AB∥CD,
证明:∵AB∥CD,∴∠DCO=∠CAB,∠CDO=∠DBA,
∵∠CAB=∠DBA,
∴OA=OB,∠DCO=∠CDO,
∴OC=OD,
在△DOA和△COB中,
|
∴△DOA≌△COB(SAS),
∵AD=BC,
∵四边形ABCD是梯形,
∴四边形ABCD是等腰梯形.
点评:本题考查了平行线的性质,全等三角形的性质和判定,等腰三角形的判定,等腰梯形的判定的应用,主要考查学生的推理能力,注意:有两腰相等的梯形是等腰梯形.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 一渔船在海岛A南偏东20°方向的B处遇险,测得海岛A与B的距离为20
一渔船在海岛A南偏东20°方向的B处遇险,测得海岛A与B的距离为20 已知:抛物线经过A(2,0)、B(8,0)、C(0,
已知:抛物线经过A(2,0)、B(8,0)、C(0, 如图,是一块电脑主板的示意图(单位:mm),其中每个角都是直角,则这块主板的周长是
如图,是一块电脑主板的示意图(单位:mm),其中每个角都是直角,则这块主板的周长是 利用如图6×4的正方形网格,计算边长分别为3、5、
利用如图6×4的正方形网格,计算边长分别为3、5、