题目内容

13．如图，已知直线AB∥CD，∠1=80°，那么∠2=100°．

分析 由直线AB∥CD，根据两直线平行，同位角相等，即可求得∠3的度数，又由邻补角的定义，即可求得答案．

解答 解：∵AB∥CD，∠1=80°，
∴∠3=∠1=80°，
又∵∠2+∠3=180°，
∴∠2=100°，
故答案为：100°．

点评 此题考查了平行线的性质．解题时注意：两直线平行，同位角相等．

练习册系列答案
相关题目
3．下列语句正确的是（　　）
A．-3是27的负的立方根B．（-1）2的平方根是-1
C．$\sqrt{64}$的立方根是2D．（-1）2的立方根是-1
4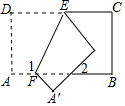．如图，把一张长方形纸片ABCD沿EF折叠后，若∠2=40°，则∠1的度数为（　　）
A．110°B．115°C．125°D．130°
1．在横线上填适当的数，使等式成立x2+6x+9=（x+3）2．
8．若关于x的一元二次方程（k-1）x2+4x+1=0有两个不相等的实数根，则k的取值范围是（　　）
A．k＜5B．k＜5且k≠1C．k≤5且k≠1D．k＞5
18．已知x2-3x+1=0，求x2+$\frac{1}{{x}^{2}}$-2（x+$\frac{1}{x}$）的值．
5．已知二次函数y=（k-2）x2+2x+1的图象与x轴有交点，则k的取值范围是（　　）
A．k≥3B．k＜3C．k≤3且k≠2D．k＜2
2．（1）计算：|-$\sqrt{2}$|+（π-3）0+（$\frac{1}{2}$）-1-2cos45°
（2）若关于x的一元二次方程x2+（k+3）x+k=0的一个根是-2，求方程的另一个根．
3．解下列方程．
（1）x（x-2）-（x-2）=0；
（2）x2+x=1．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网