题目内容
18.已知x2-3x+1=0,求x2+$\frac{1}{{x}^{2}}$-2(x+$\frac{1}{x}$)的值.分析 首先由x2-3x-1=0两边同除以x得出x+$\frac{1}{x}$=3,进一步配方求得答案即可.
解答 解:将x2-3x+1=0两边同时除以x,得x+$\frac{1}{x}$=3,
∴x2+$\frac{1}{{x}^{2}}$-2(x+$\frac{1}{x}$)
=(x+$\frac{1}{x}$)2-2--2(x+$\frac{1}{x}$)
=32-2-2×3
=1
点评 此题考查等式的性质以及代数式求值,注意根据所给的条件,适当变形,利用配方法解决问题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9.在Rt△ABC中,∠C=90°,AB=2,BC=1,则AC的长为( )
| A. | 1 | B. | $\sqrt{3}$ | C. | $\sqrt{5}$ | D. | 3 |
3.已知2是关于x的方程x2-ax+2=0的一个根,则另一个根为( )
| A. | 1 | B. | 2 | C. | -1 | D. | -2 |
10.若关于x的方程x2+3x+a=0有一个根为-1,则a的值为( )
| A. | 2 | B. | -1 | C. | -2 | D. | 1 |
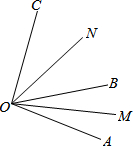 已知,如图,OM平分∠AOB,ON平分∠BOC.
已知,如图,OM平分∠AOB,ON平分∠BOC. 如图,已知直线AB∥CD,∠1=80°,那么∠2=100°.
如图,已知直线AB∥CD,∠1=80°,那么∠2=100°. 如图,在对Rt△ABC依次进行轴对称(对称轴为y轴)、一次平移和以O为位似中心在同侧缩小为原来的一半的变换后得到△OA′B′.
如图,在对Rt△ABC依次进行轴对称(对称轴为y轴)、一次平移和以O为位似中心在同侧缩小为原来的一半的变换后得到△OA′B′.