题目内容
5.已知二次函数y=(k-2)x2+2x+1的图象与x轴有交点,则k的取值范围是( )| A. | k≥3 | B. | k<3 | C. | k≤3且k≠2 | D. | k<2 |
分析 根据二次函数图象与x轴有交点可得出关于x的一元二次方程有解,根据根的判别式结合二次项系数非零即可得出关于k的一元一次不等式组,解不等式组即可得出结论.
解答 解:∵二次函数y=(k-2)x2+2x+1的图象与x轴有交点,
∴一元二次方程(k-2)x2+2x+1=0有解,
∴$\left\{\begin{array}{l}{k-2≠0}\\{△={2}^{2}-4(k-2)=12-4k≥0}\end{array}\right.$,
解得:k≤3且k≠2.
故选:C.
点评 本题考查了抛物线与x轴的交点、根的判别式以及解一元一次不等式组,根据根的判别式△≥0结合二次项系数非零找出关于k的一元一次不等式组是解题的关键.

练习册系列答案
相关题目
20.若|x+y-3|+$\sqrt{2x-y}$=0,则x-y的值为( )
| A. | -1 | B. | 1 | C. | 2 | D. | -2 |
10.若关于x的方程x2+3x+a=0有一个根为-1,则a的值为( )
| A. | 2 | B. | -1 | C. | -2 | D. | 1 |
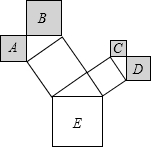 如图是一株美丽的勾股树,所有的四边形都是正方形,所有的三角形都是直角三角形.其中最大的直角三角形两直角边长分别为2,3,则正方形A,B,C,D的面积之和为( )
如图是一株美丽的勾股树,所有的四边形都是正方形,所有的三角形都是直角三角形.其中最大的直角三角形两直角边长分别为2,3,则正方形A,B,C,D的面积之和为( ) 如图,已知直线AB∥CD,∠1=80°,那么∠2=100°.
如图,已知直线AB∥CD,∠1=80°,那么∠2=100°.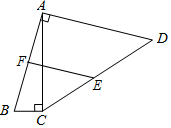 如图,四边形ABCD中,AB=AD,∠ACB=∠BAD=90°,E、F分别为CD、AB的中点,BC=2,CD=2$\sqrt{13}$,则EF=$\sqrt{17}$.
如图,四边形ABCD中,AB=AD,∠ACB=∠BAD=90°,E、F分别为CD、AB的中点,BC=2,CD=2$\sqrt{13}$,则EF=$\sqrt{17}$.