题目内容
8.若关于x的一元二次方程(k-1)x2+4x+1=0有两个不相等的实数根,则k的取值范围是( )| A. | k<5 | B. | k<5且k≠1 | C. | k≤5且k≠1 | D. | k>5 |
分析 根据一元二次方程的定义和判别式的意义得到k-1≠0且△=42-4(k-1)×1>0,然后求出两个不等式的公共部分即可.
解答 解:根据题意得k-1≠0且△=42-4(k-1)×1>0,
解得:k<5且k≠1.
故选B.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.当x=1时,ax3-2bx+3=6,则当x=-1时,这个代数式的值是( )
| A. | 6 | B. | 0 | C. | -6 | D. | -3 |
3.下列方程中,是关于x的一元一次方程的是( )
| A. | x=0 | B. | $\frac{1}{x}$+x=2 | C. | x(x-1)=1 | D. | $\frac{x}{2}$+$\frac{3x}{2}$+1=2(x-1) |
20.若|x+y-3|+$\sqrt{2x-y}$=0,则x-y的值为( )
| A. | -1 | B. | 1 | C. | 2 | D. | -2 |
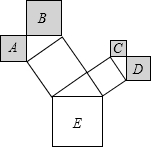 如图是一株美丽的勾股树,所有的四边形都是正方形,所有的三角形都是直角三角形.其中最大的直角三角形两直角边长分别为2,3,则正方形A,B,C,D的面积之和为( )
如图是一株美丽的勾股树,所有的四边形都是正方形,所有的三角形都是直角三角形.其中最大的直角三角形两直角边长分别为2,3,则正方形A,B,C,D的面积之和为( ) 如图,已知直线AB∥CD,∠1=80°,那么∠2=100°.
如图,已知直线AB∥CD,∠1=80°,那么∠2=100°.