题目内容

3．下列语句正确的是（　　）
A．-3是27的负的立方根B．（-1）2的平方根是-1
C．$\sqrt{64}$的立方根是2D．（-1）2的立方根是-1

分析 根据平方根，立方根的意义，可得答案．

解答 解：A、-3时-27的立方根，故A不符合题意；
B、（-1）2的平方根是±1，故B不符合题意；
C、$\sqrt{64}$=8，$\sqrt{64}$的立方根是$\root{3}{8}$=2，故C符合题意；
D、（-1）2的立方根是1，故D不符合题意；
故选：C．

点评 本题考查了实数，利用平方根，立方根的意义是解题关键．

练习册系列答案
相关题目
13．一元二次方程5x2-2x=0的解是（　　）
A．x1=0，x2=$\frac{2}{5}$B．x1=0，x2=-$\frac{2}{5}$C．x1=0，x2=$\frac{5}{2}$D．x1=0，x2=-$\frac{5}{2}$
14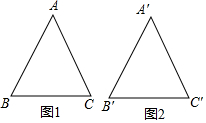．已知△ABC如图1所示，平平通过作图得到如图2所示的△A′B′C，其作图步骤为：
①画B′C′=BC；
②分别以点B′C′为圆心，线段AB，AC长为半径画弧，两弧交于点A′；
③连接A′B′，A′C′，则判断△ABC≌△A′B′C′的依据是（　　）
A．SSSB．SASC．ASAD．AAS
11．下列等式变形正确的是（　　）
A．若1-2x=6，则2x=6-1B．若$\frac{1}{2}$x=6，则x=3
C．若x-3=y-3，则x-y=0D．若mx=my，则x=y
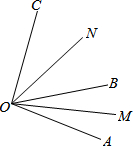18．如果关于x，y的二元一次方程组$\left\{\begin{array}{l}{3x-ay=16}\\{2x+by=15}\end{array}\right.$的解是$\left\{\begin{array}{l}{x=7}\\{y=1}\end{array}\right.$，那么关于m，n的二元一次方程组$\left\{\begin{array}{l}{3（m+n）-a（m-n）=16}\\{2（m+n）+b（m-n）=15}\end{array}\right.$的解是$\left\{\begin{array}{l}{m=4}\\{n=3}\end{array}\right.$．
8．已知，如图，OM平分∠AOB，ON平分∠BOC．
（1）当∠AOC=90°，∠BOC=60°时，求∠MON的度数；
（2）当∠AOC=86°，∠BOC=60°时，求∠MON的度数；
（3）当∠AOC=80°，∠BOC=50°时，求∠MON的度数；
（4）猜想不论∠AOC和∠BOC的度数是多少，∠MON的度数总等于∠AOC度数的一半，并说明理由．
15．一点A从数轴上表示+2的A点开始移动，第一次先向左平移1个单位，再向右平移2个单位；第二次先向左移动3个单位，再向右移动4个单位；第三次先向左移动5个单位，再向右移动6个单位．求：
（1）写出第一次移动后这个点在数轴上表示的数为+3；
（2）写出第二次移动结果这个点在数轴上表示的数为+4；
（3）写出第三次移动后这个点在数轴上表示的数+5．
（4）写出第n次移动结果这个点在数轴上表示的数2+n．
12．今年以来，我国持续大面积的雾霾天气让环保和健康问题成为焦点．为了调查学生对雾霾天气知识的了解程度，重庆一中在初三学生中做了一次抽样调查，调查结果共分为四个等级：A．非常了解；B．比较了解；C．基本了解；D．不了解．根据调查统计结果，绘制了不完整的两种统计图表．
请结合统计图表，回答下列问题．

（1）本次参与调查的学生共有400人，图2所示的扇形统计图中B部分对应的圆心角是54度，请补全图1所示的条形统计图；
（2）如果学校共有学生4800名，那么请你估计不了解雾霾天气知识的学生人数．
13．如图，已知直线AB∥CD，∠1=80°，那么∠2=100°．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网