题目内容
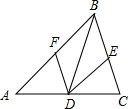 如图,△ABC中,BD平分∠ABC,过D作DE∥AB交BC于E,DF∥BC交AB于F.
如图,△ABC中,BD平分∠ABC,过D作DE∥AB交BC于E,DF∥BC交AB于F.求证:四边形BFDE为菱形.
考点:菱形的判定
专题:证明题
分析:首先根据DE∥AB,DF∥BC,可得四边形BFDE是平行四边形,再证明FB=FD,可得四边形BFDE为菱形.
解答: 证明:∵DE∥AB,DF∥BC,
证明:∵DE∥AB,DF∥BC,
∴四边形BFDE是平行四边形,
∵BD平分∠ABC,
∴∠1=∠2,
∵AB∥DE,
∴∠3=∠2,
∴∠1=∠3,
∴FB=FD,
∴四边形BFDE为菱形.
 证明:∵DE∥AB,DF∥BC,
证明:∵DE∥AB,DF∥BC,∴四边形BFDE是平行四边形,
∵BD平分∠ABC,
∴∠1=∠2,
∵AB∥DE,
∴∠3=∠2,
∴∠1=∠3,
∴FB=FD,
∴四边形BFDE为菱形.
点评:此题主要考查了菱形的判定,关键是掌握一组邻边相等的平行四边形是菱形.

练习册系列答案
相关题目
在Rt△ABC中,∠C=90°,则tanA•tanB等于( )
| A、0 | B、1 | C、-1 | D、不确定 |
若
与
化成最简二次根式是可以合并的,则m、n的值为( )
| m+n | 4n |
| 27m+9n |
| A、m=0,n=2 |
| B、m=1,n=1 |
| C、m=0,n=2或m=1,n=1 |
| D、m=2,n=0 |
下列计算中正确的是( )
| A、a6+b6=a12 |
| B、(ab)3=ab3 |
| C、(a-b)(-a-b)=-a2+b2 |
| D、(x-3y)2=x2-3xy+9y2 |
 在△ABC中,点D、E分别在AB、AC边上,连结DE,要使△ADE与△ABC相似,应添加的条件是
在△ABC中,点D、E分别在AB、AC边上,连结DE,要使△ADE与△ABC相似,应添加的条件是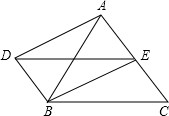 如图,DB∥AC,且DB=
如图,DB∥AC,且DB= 如图,已知AB=AC,BD⊥AC于点D,求证:∠DBC=
如图,已知AB=AC,BD⊥AC于点D,求证:∠DBC=