题目内容
2.已知直角三角形的周长为14,斜边上的中线长为3.则直角三角形的面积是7.分析 由∠ACB=90°,CD是斜边上的中线,求出AB=6,根据AB+AC+BC=14,求出AC+BC,根据勾股定理得出AC2+BC2=AB2=36推出AC•BC=14,根据S=$\frac{1}{2}$AC•BC即可求出答案.
解答 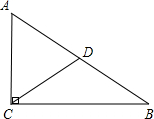 解:如图,∵∠ACB=90°,CD是斜边上的中线,
解:如图,∵∠ACB=90°,CD是斜边上的中线,
∴AB=2CD=6,
∵AB+AC+BC=14,
∴AC+BC=8,
由勾股定理得:AC2+BC2=AB2=36,
∴(AC+BC)2-2AC•BC=36,
AC•BC=14,
∴S=$\frac{1}{2}$AC•BC=7.
故答案为:7.
点评 本题主要考查对直角三角形斜边上的中线,勾股定理,三角形的面积等知识点的理解和掌握,能根据性质求出AC•BC的值是解此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.如果把分式-$\frac{3xy}{x+y}$中的x和y都扩大3倍,即分式的值( )
| A. | 扩大3倍 | B. | 扩大9倍 | C. | 不变 | D. | 缩小9倍 |
11. 如图,点A、B、C、P在⊙O上,CD⊥OA,CE⊥OB,垂足分别为D,E,∠DCE=40°,则∠P的度数为( )
如图,点A、B、C、P在⊙O上,CD⊥OA,CE⊥OB,垂足分别为D,E,∠DCE=40°,则∠P的度数为( )
 如图,点A、B、C、P在⊙O上,CD⊥OA,CE⊥OB,垂足分别为D,E,∠DCE=40°,则∠P的度数为( )
如图,点A、B、C、P在⊙O上,CD⊥OA,CE⊥OB,垂足分别为D,E,∠DCE=40°,则∠P的度数为( )| A. | 70° | B. | 60° | C. | 40° | D. | 35° |
 如图,已知在△ABC中,AD是BC边上的中线,E是AD的中点,连接BE并延长交AC于点F,G是BF的中点.求证:
如图,已知在△ABC中,AD是BC边上的中线,E是AD的中点,连接BE并延长交AC于点F,G是BF的中点.求证: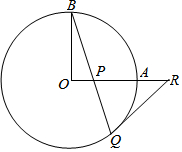 如图,OA和OB是⊙O的半径,并且OA⊥OB.P是OA上任意一点,BP的延长线交⊙O于点Q,点R在OA的延长线上,且RP=RQ.
如图,OA和OB是⊙O的半径,并且OA⊥OB.P是OA上任意一点,BP的延长线交⊙O于点Q,点R在OA的延长线上,且RP=RQ.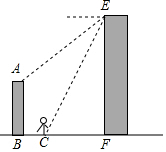 为纪念京汉铁路工人大罢工而修建的二七纪念塔于去年下半年重新整修,一装修工在塔EF的顶部处测得对面一栋AB=9米高的楼房顶部A的俯角为45°,测得楼房正前方BC=7米处一站牌底部C点的俯角为60°,请你帮助装修工人计算塔的高度是多少?($\sqrt{3}$≈1.732,结果保留到1米.)
为纪念京汉铁路工人大罢工而修建的二七纪念塔于去年下半年重新整修,一装修工在塔EF的顶部处测得对面一栋AB=9米高的楼房顶部A的俯角为45°,测得楼房正前方BC=7米处一站牌底部C点的俯角为60°,请你帮助装修工人计算塔的高度是多少?($\sqrt{3}$≈1.732,结果保留到1米.)