题目内容
11．
如图，点A、B、C、P在⊙O上，CD⊥OA，CE⊥OB，垂足分别为D，E，∠DCE=40°，则∠P的度数为（ ）| A． | 70° | B． | 60° | C． | 40° | D． | 35° |
分析 先根据四边形内角和定理求出∠DOE的度数，再由圆周角定理即可得出结论．
解答 解：∵CD⊥OA，CE⊥OB，垂足分别为D，E，∠DCE=40°，
∴∠DOE=180°-40°=140°，
∴∠P=$\frac{1}{2}$∠DOE=70°．
故选A．
点评 本题考查的是圆周角定理，熟知在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半是解答此题的关键．
练习册系列答案
相关题目
19．
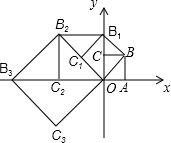如图，在平面直角坐标系中有一边长为1的正方形OABC，边OA、OC分别在x轴、y轴上，如果以对角线OB为边作第二个正方形OBB1C1，再以对角线OB1为边作第三个正方形OB1B2C2，照此规律作下去，则点B2015的坐标为（ ）
如图，在平面直角坐标系中有一边长为1的正方形OABC，边OA、OC分别在x轴、y轴上，如果以对角线OB为边作第二个正方形OBB1C1，再以对角线OB1为边作第三个正方形OB1B2C2，照此规律作下去，则点B2015的坐标为（ ）| A． | （21008，0） | B． | （21007，-21007） | C． | （21009，21009） | D． | （-21007，21007） |
6．
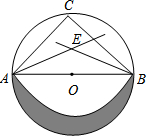如图，⊙O的直径AB=2，C是弧AB的中点，AE，BE分别平分∠BAC和∠ABC，以E为圆心，AE为半径作扇形EAB，π取3，则阴影部分的面积为（ ）
如图，⊙O的直径AB=2，C是弧AB的中点，AE，BE分别平分∠BAC和∠ABC，以E为圆心，AE为半径作扇形EAB，π取3，则阴影部分的面积为（ ）| A． | $\frac{13}{4}$$\sqrt{2}$-4 | B． | 7$\sqrt{2}$-4 | C． | 6-$\frac{5}{4}$$\sqrt{2}$ | D． | $\frac{{3\sqrt{2}-5}}{2}$ |
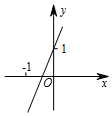
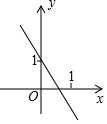
已知函数y=kx+b（k≠0）的图象如图，则y=-2kx+b（k≠0）的图象可能是（ ）
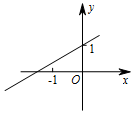
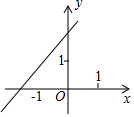
如图，在直角坐标系中，点A是反比例函数y1=$\frac{k}{x}$图象上一点，AB⊥x轴的正半轴于点B，点C是OB的中点，一次函数y2=ax+b的图象经过A、C两点，交y轴于点D（0，-2），△AOB的面积为4