题目内容
17. 如图,已知在△ABC中,AD是BC边上的中线,E是AD的中点,连接BE并延长交AC于点F,G是BF的中点.求证:
如图,已知在△ABC中,AD是BC边上的中线,E是AD的中点,连接BE并延长交AC于点F,G是BF的中点.求证:(1)AF=$\frac{1}{2}$FC;
(2)四边形AGDF是平行四边形.
分析 (1)先根据中位线定理证明DG∥AC,再利用△AEF≌△DEG(AAS),得GD=AF,所以AF=$\frac{1}{2}$FC;
(2)根据(1)中的一组对边平行且相等得结论.
解答 证明:(1)∵AD是BC边上的中线,
∴BD=DC,
∵G是BF的中点,
∴DG是△BFC的中位线,
∴DG∥AC,DG=$\frac{1}{2}$FC,
∴∠GDE=∠EAF,
∵E是AD的中点,
∴AE=ED,
在△AEF和△DEG中,
∵$\left\{\begin{array}{l}{∠GDE=∠EAF}\\{∠GED=∠FEA}\\{ED=AE}\end{array}\right.$,
∴△AEF≌△DEG(AAS),
∴GD=AF,
∴AF=$\frac{1}{2}$FC;
(2)由(1)得:GD∥AF,GD=AF,
∴四边形AGDF是平行四边形.
点评 本题考查了平行四边形的判定、三角形中位线定理、三角形全等的性质和判定,熟练掌握和运用三角形的中位线定理是本题的关键.

练习册系列答案
相关题目
12.下列各式中,计算的结果为负数的是( )
| A. | $\root{3}{125}$ | B. | -32 | C. | $\sqrt{16}$ | D. | $\sqrt{\frac{1}{4}}$ |
6.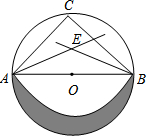 如图,⊙O的直径AB=2,C是弧AB的中点,AE,BE分别平分∠BAC和∠ABC,以E为圆心,AE为半径作扇形EAB,π取3,则阴影部分的面积为( )
如图,⊙O的直径AB=2,C是弧AB的中点,AE,BE分别平分∠BAC和∠ABC,以E为圆心,AE为半径作扇形EAB,π取3,则阴影部分的面积为( )
 如图,⊙O的直径AB=2,C是弧AB的中点,AE,BE分别平分∠BAC和∠ABC,以E为圆心,AE为半径作扇形EAB,π取3,则阴影部分的面积为( )
如图,⊙O的直径AB=2,C是弧AB的中点,AE,BE分别平分∠BAC和∠ABC,以E为圆心,AE为半径作扇形EAB,π取3,则阴影部分的面积为( )| A. | $\frac{13}{4}$$\sqrt{2}$-4 | B. | 7$\sqrt{2}$-4 | C. | 6-$\frac{5}{4}$$\sqrt{2}$ | D. | $\frac{{3\sqrt{2}-5}}{2}$ |
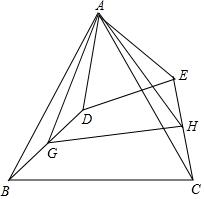 如图,△ABC中,AB=AC,∠BAC=α°(α为已知常数),以A为顶点作△ADE,使∠BAC=∠DAE,AD=AE,G、H分别为BD、CE的中点.
如图,△ABC中,AB=AC,∠BAC=α°(α为已知常数),以A为顶点作△ADE,使∠BAC=∠DAE,AD=AE,G、H分别为BD、CE的中点.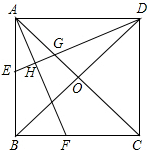 已知,如图,在正方形ABCD中,O是对角线的交点,AF平分∠BAC,DH⊥AF于点H,交AC于点G,DH延长线交AB于点E.
已知,如图,在正方形ABCD中,O是对角线的交点,AF平分∠BAC,DH⊥AF于点H,交AC于点G,DH延长线交AB于点E.