题目内容
下列函数中,具有过原点,且当x>0时,y随x增大而减小,这两个特征的有( )
①y=-ax2(a>0);②y=(a-1)x2(a<1);③y=-2x+a2(a≠0);④y=
x-a(a≠0).
①y=-ax2(a>0);②y=(a-1)x2(a<1);③y=-2x+a2(a≠0);④y=
| 3 |
| 2 |
| A、1个 | B、2个 | C、3个 | D、4个 |
考点:二次函数的性质,一次函数的性质
专题:
分析:根据二次函数的性质对各选项进行逐一分析即可.
解答:解:①∵y=-ax2(a>0)中a>0,
∴-a<0,
∴此函数图象过原点,且当x>0时,y随x增大而减小,故本小题正确;
②∵y=(a-1)x2(a<1),
∴a-1<0,
∴此函数图象过原点,且当x>0时,y随x增大而减小,故本小题正确;
③∵y=-2x+a2(a≠0)中,a≠0,
∴此函数的图象不过原点,故本小题错误;
④∵y=
x-a(a≠0)中a≠0,
∴此函数的图象不过原点,故本小题错误.
故选B.
∴-a<0,
∴此函数图象过原点,且当x>0时,y随x增大而减小,故本小题正确;
②∵y=(a-1)x2(a<1),
∴a-1<0,
∴此函数图象过原点,且当x>0时,y随x增大而减小,故本小题正确;
③∵y=-2x+a2(a≠0)中,a≠0,
∴此函数的图象不过原点,故本小题错误;
④∵y=
| 3 |
| 2 |
∴此函数的图象不过原点,故本小题错误.
故选B.
点评:本题考查的是二次函数的性质,熟知二次函数的图象与系数的关系及二次函数的增减性是解答此题的关键.

练习册系列答案
相关题目
 如图,经过⊙O上点A的切线和弦BC的延长线相交于点P,若∠CAP=40°,∠ACP=100°,则∠BAC的度数为( )
如图,经过⊙O上点A的切线和弦BC的延长线相交于点P,若∠CAP=40°,∠ACP=100°,则∠BAC的度数为( )| A、40° | B、60° |
| C、80° | D、70° |
 如图,以直角三角形的三条边为边分别向外作正方形,求图中字母所代表的正方形面积.
如图,以直角三角形的三条边为边分别向外作正方形,求图中字母所代表的正方形面积. 如图,等腰△ACB中,AB=AC.直线AD是它的对称轴;DE⊥AC于E,DF⊥AB于F,则图中直角三角形有
如图,等腰△ACB中,AB=AC.直线AD是它的对称轴;DE⊥AC于E,DF⊥AB于F,则图中直角三角形有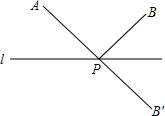 如图,点A、B在直线l的同侧,点B′是B点关于l的对称点,AB′交l于点P.
如图,点A、B在直线l的同侧,点B′是B点关于l的对称点,AB′交l于点P.